基于MLP人工神经网络理论构建数学模型 人工神经网络题目

如下是 2020年人工神经网络第二次作业 中第五题的参考答案。

 

➤01 第五题参考答案

---

1.题目分析

(1) 数据产生

100个样本随机均匀分布在三角形区域内，训练样本$\left\{ {x_i ,y_i } \right\}$满足：
$x_i \in \left( {0,1} \right),\,\,y_i < \sqrt 3 \left( {0.5 - \left| {x - 0.5} \right|} \right)$

下面使用 作业中的程序中python子程序:generate_data_triangle()产生100随机分布的数据点：

^{▲ 100个数据点}

(2) 网络结构

自组织特征映射(SOFM)网络有15个竞争层的神经元，它们具有一维的拓扑结构。

^{▲ 一位拓扑结构的SOFM网络结构}

竞争层的神经元参数$\left\{ {w_{i1} ,w_{i2} } \right\}_{i = 1,2, \cdots 15}$初始化为区域$\left( {0,1} \right) \times \left( {0,\sqrt 3 /2} \right)$中的随机数。

初始化之后，竞争层的神经元所处的位置：

^{▲ 网络初始化竞争神经元所处的位置}

2.求解过程

求解过程中相关程序参见后面附录中 作业中的程序。

(1) 训练参数

• 训练半径：R从10线性递减到0
• 学习速率：$\eta$从0.3线性递减到0
• 训练周期：N= 200

(2) 学习过程

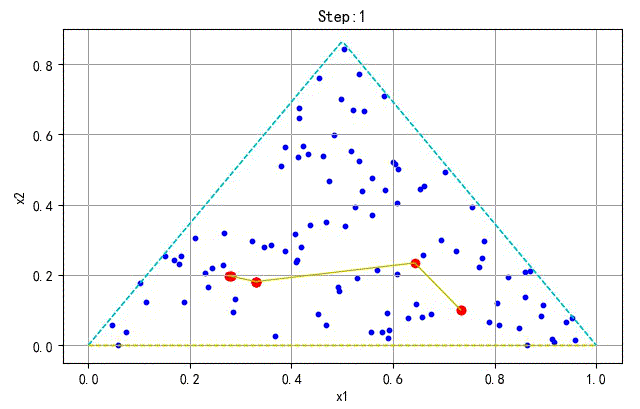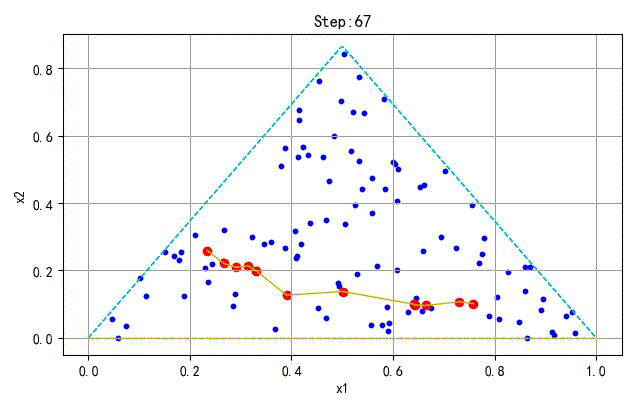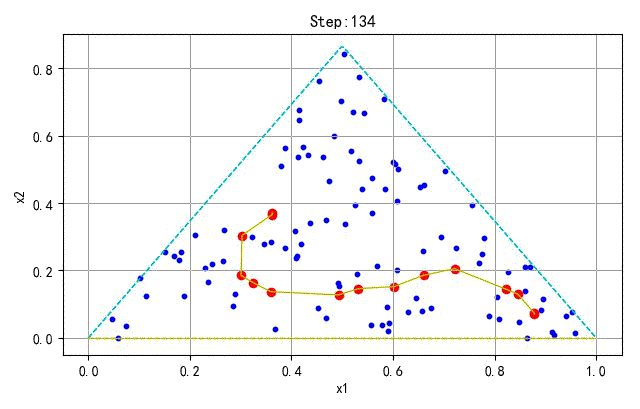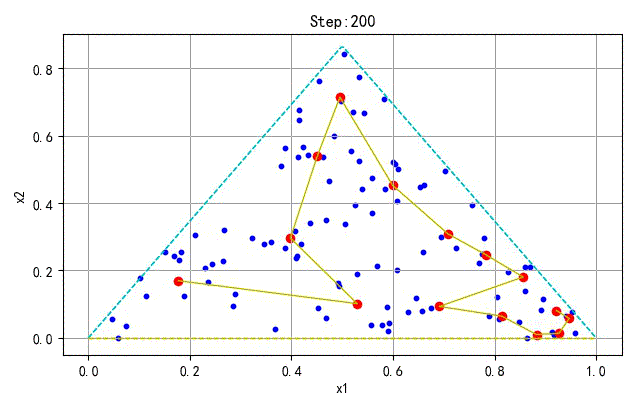
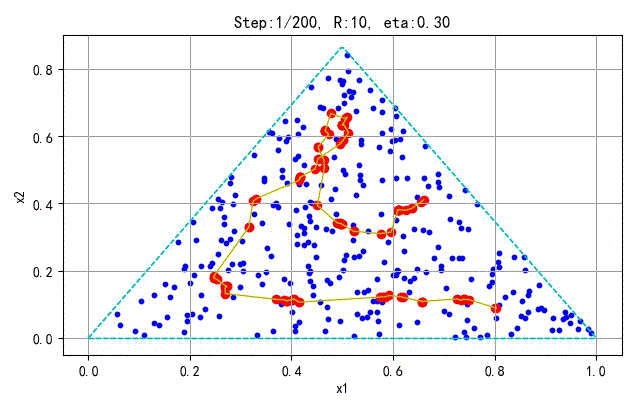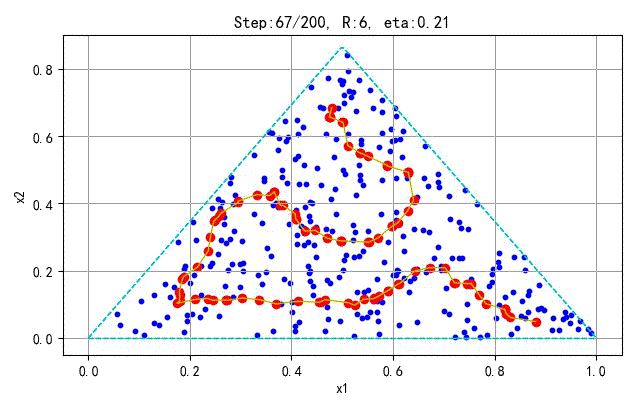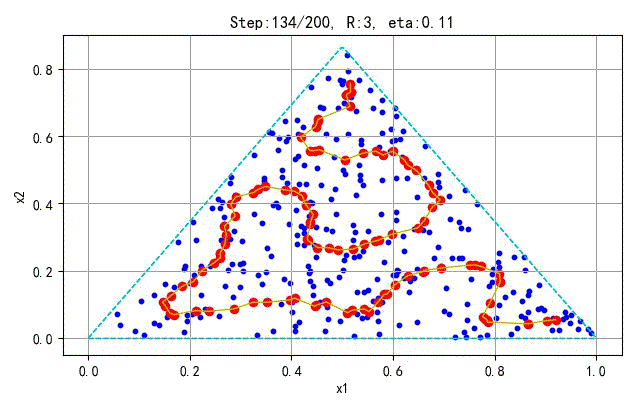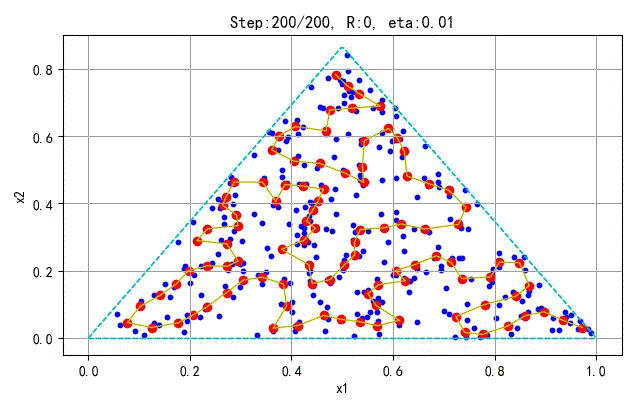
^{▲ 学习训练过程}

(3) 训练结果

下面为训练的结果。SOFM的保序特性体现在竞争层的神经元分布与训练样本分布区域保持一致。

^{▲ 训练后的结果}

3.结果讨论

为了更好地显示SOFM保序特性，下面在分别对不同的采样点和神经元个数训练的情况进行展示。训练参数（学习半径、学习速率）与前面相同。

• 训练样本：100； 神经元个数：25

• 
  

• 
  

 

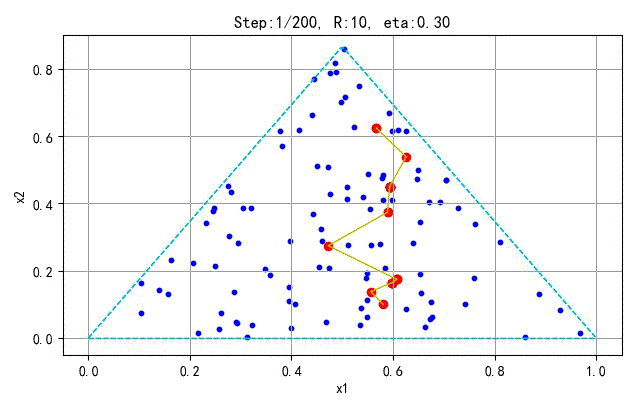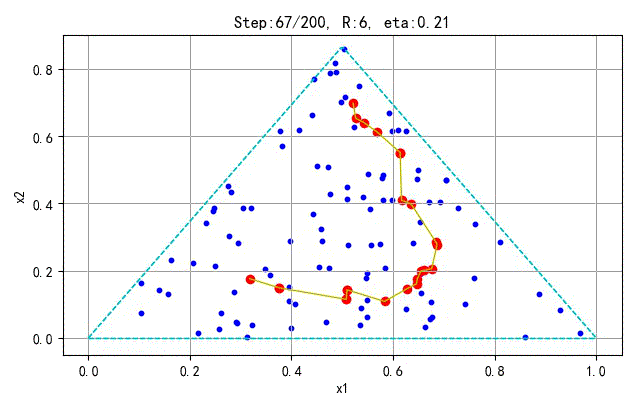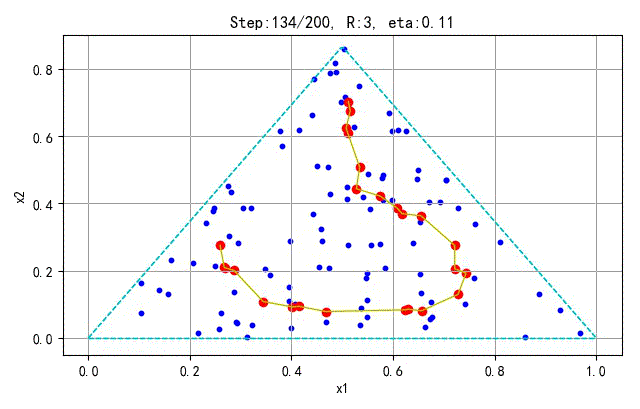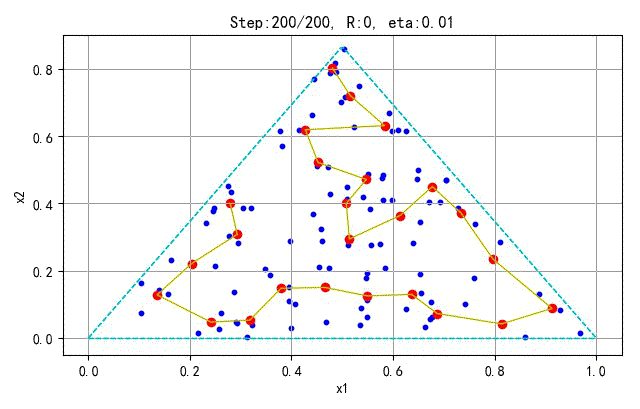
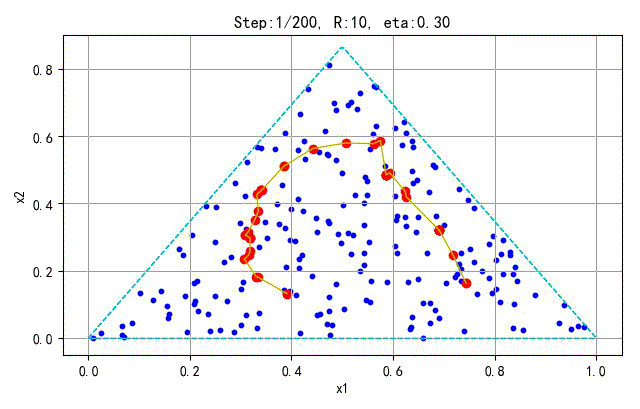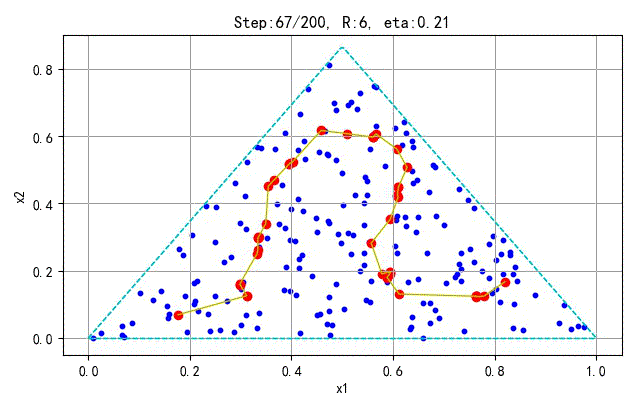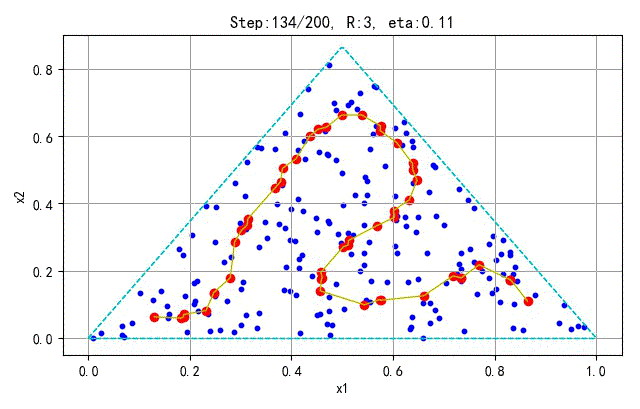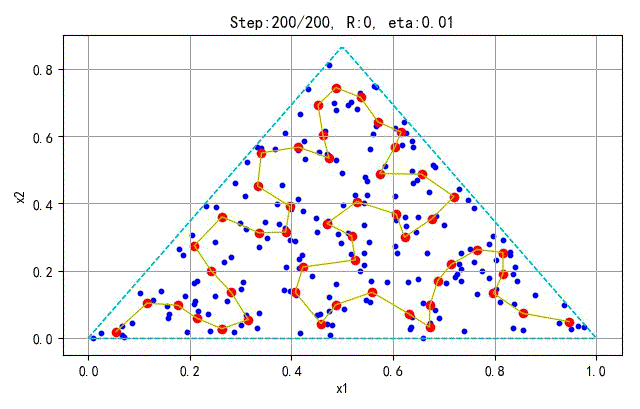
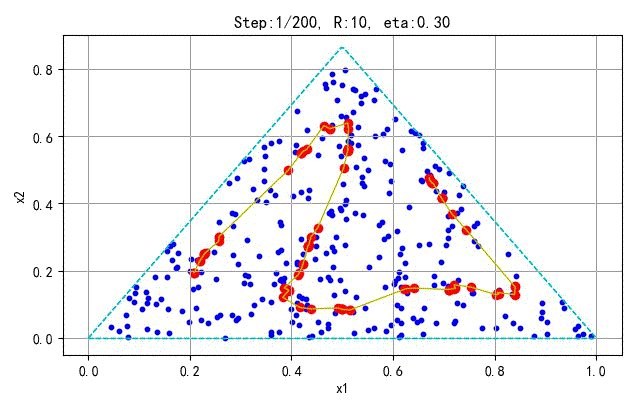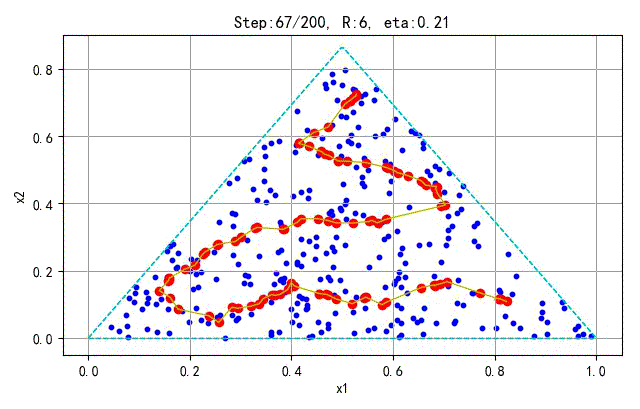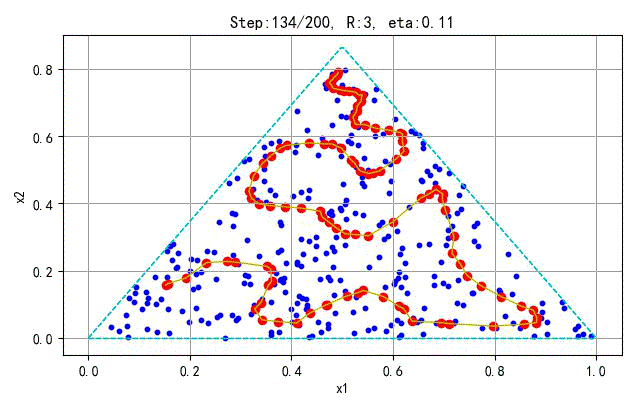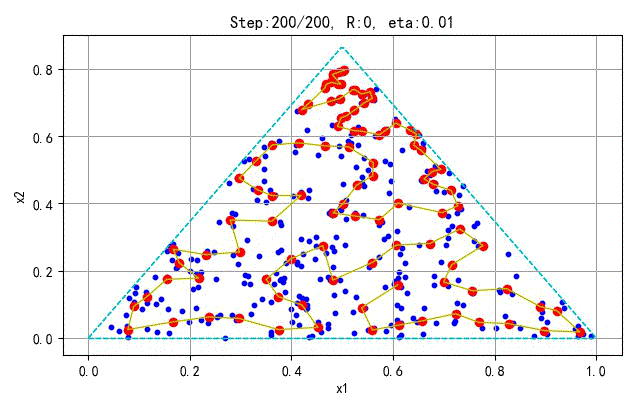
➤● 补充讨论

---

1.对2维拓扑结构SOFM进行训练

(1) 训练数据

数据采集自$\left[ { - 1,1} \right] \times \left[ { - 1,1} \right]$随机分布的点。下图显示了300个随机均匀采样后的数据点。

x_ = random.random(num)
y_ = random.random(num)
xy = vstack((x_, y_))

^{▲ 用于训练2D SOFM的数据}

(2) 神经网络初始化

W = stack((random.random((NEURAL_NUM, NEURAL_NUM)), random.random((NEURAL_NUM, NEURAL_NUM)))).T

^{▲ 随机初始化后的神经节点}

2.训练结果

(1) 训练参数

• 训练样本：N=500
• 神经元个数：10×10
• 学习速率：从0.1线性降低到0.01
• 学习半径：从3 线性降低带0
• 训练迭代次数：100

(2) 训练结果

下面是一次训练结果，2D的SOFM的神经元均匀分布在训练样本中间。

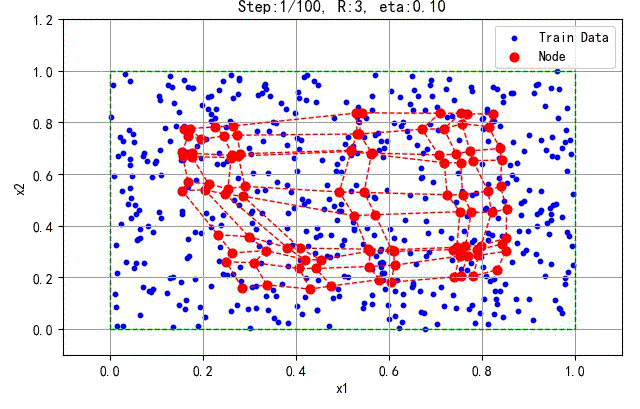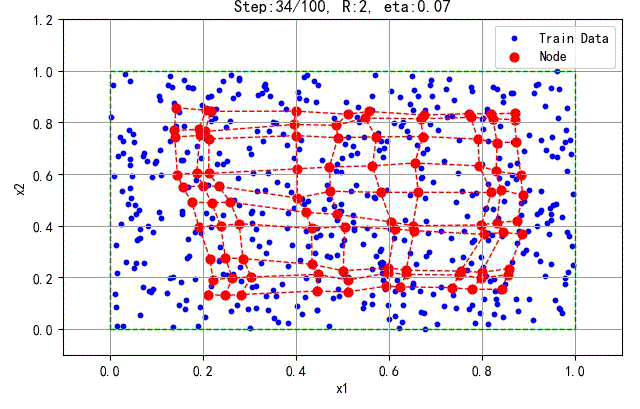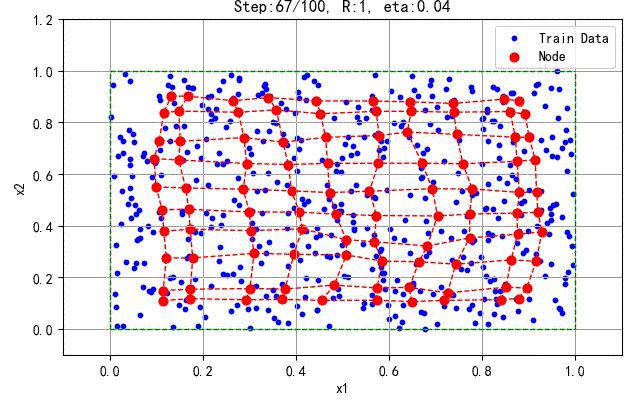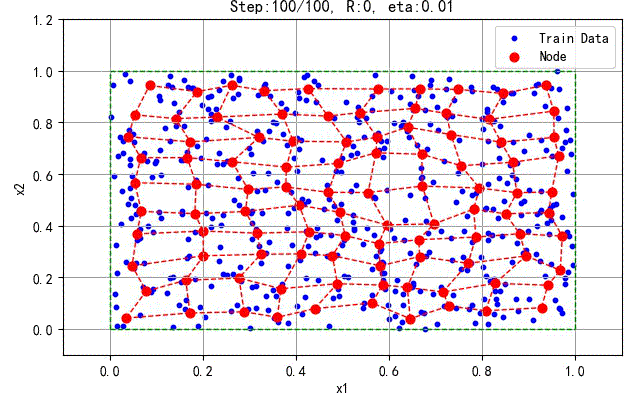
^{▲ 2D拓扑结构的SOFM的训练结果}

下面是一次训练扭曲的分布结果：

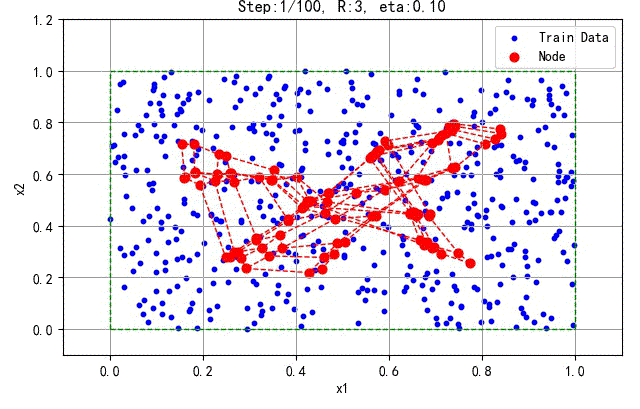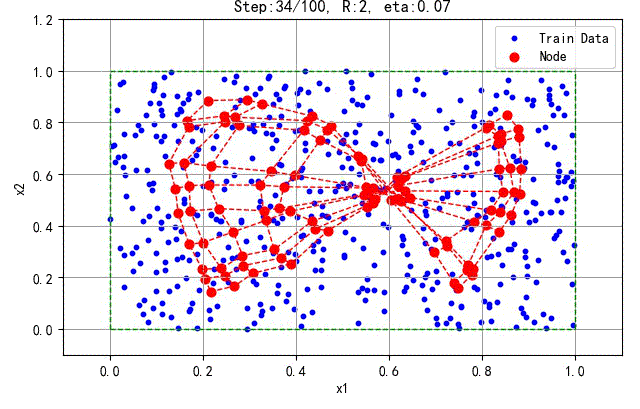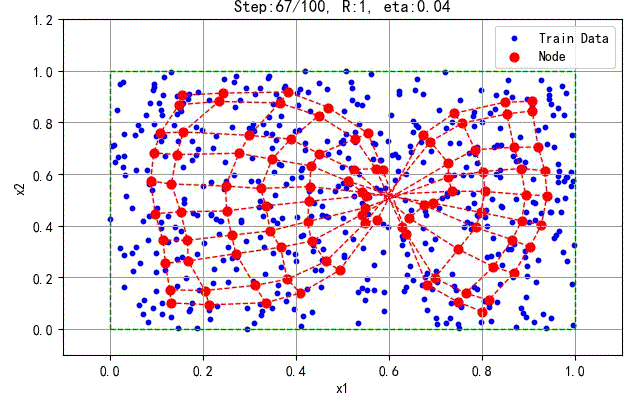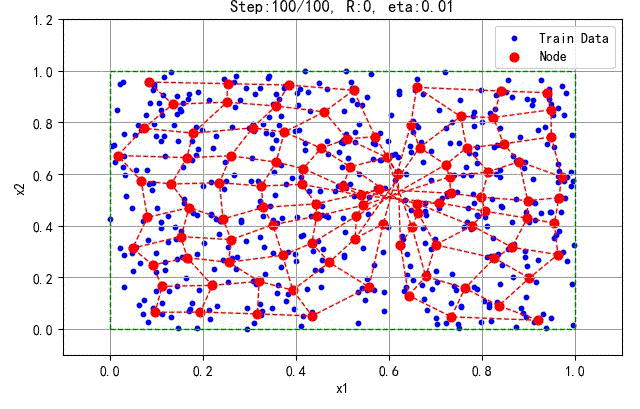
^{▲ 发生扭曲的训练过程}

3.不同的训练数据和节点个数对应的结果

(1) 较少的训练数据

下面是200 个训练数据产生的结果：

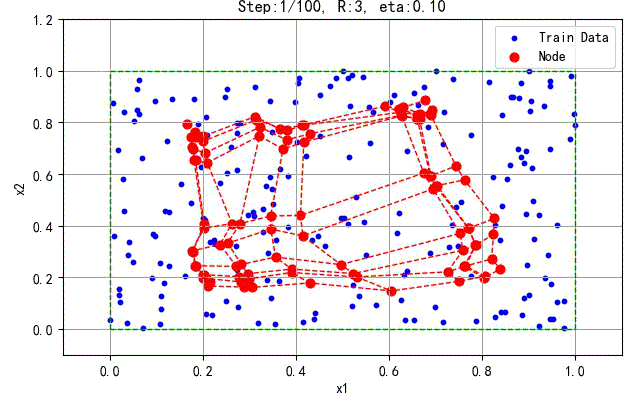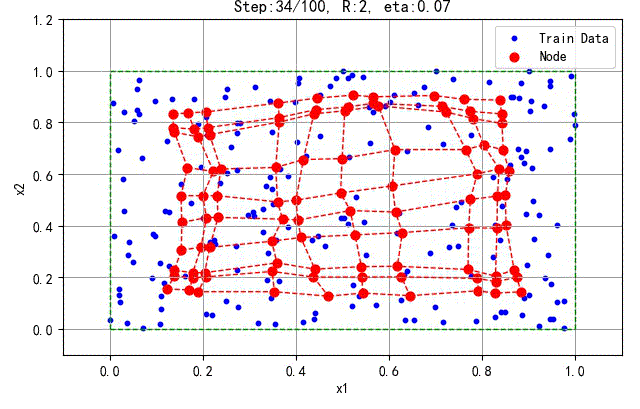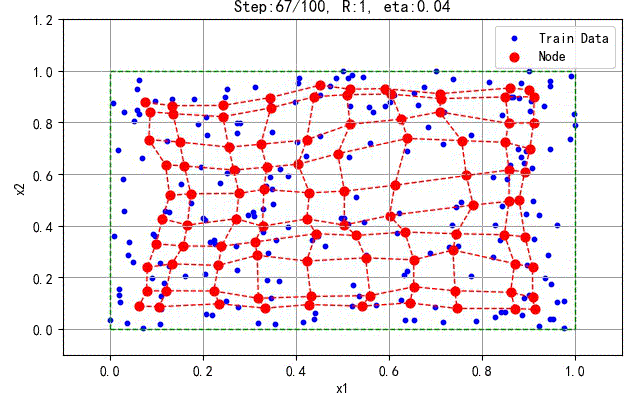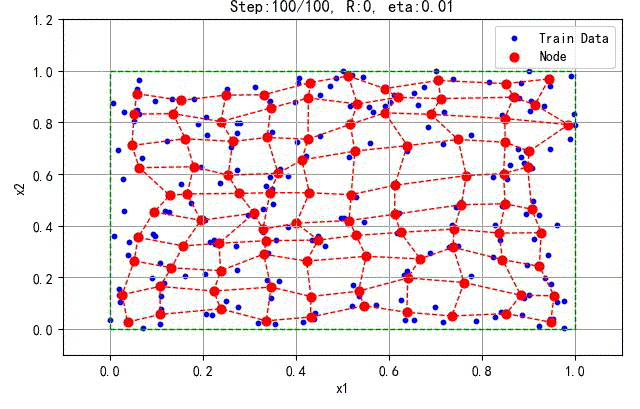
^{▲ 200个训练数据的结果}

如下是2000个数据所产生的结果：

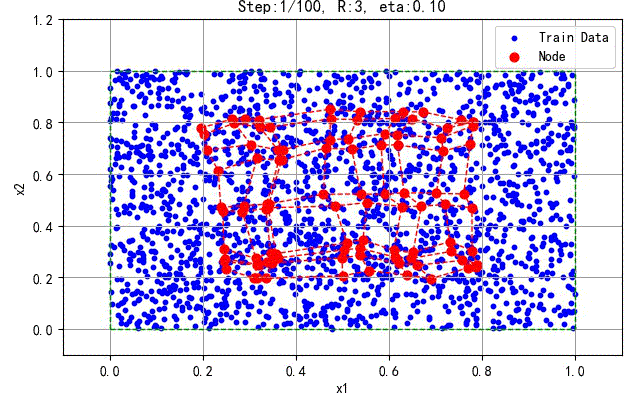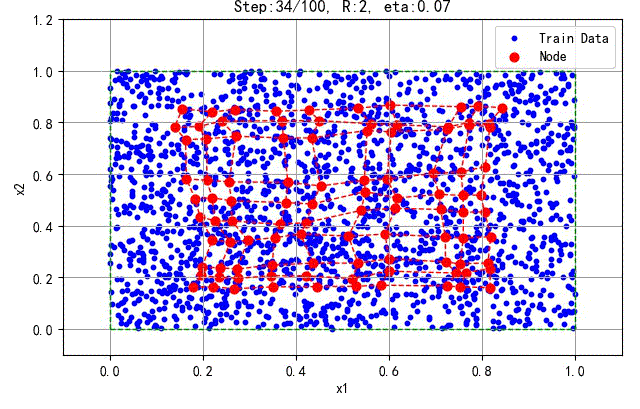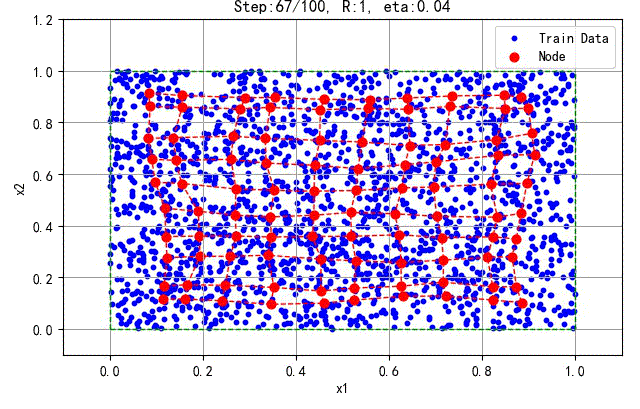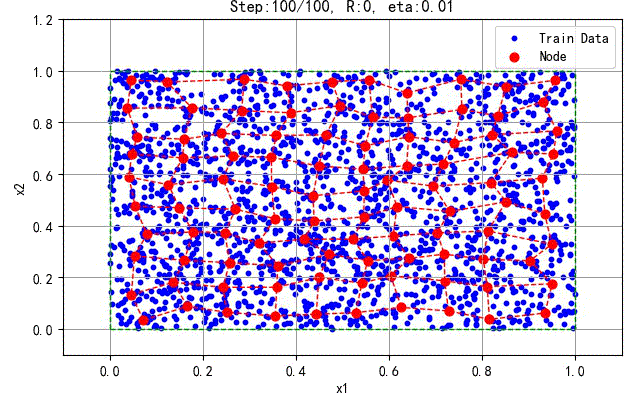
^{▲ 2000个训练数据产生的结果}

如下是200个数据训练5×5的二维结构所产生的结果：

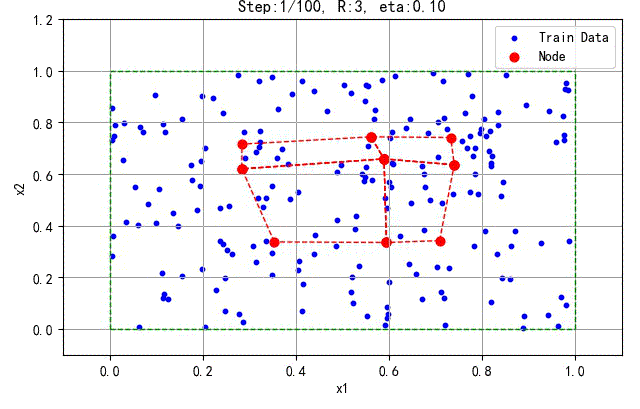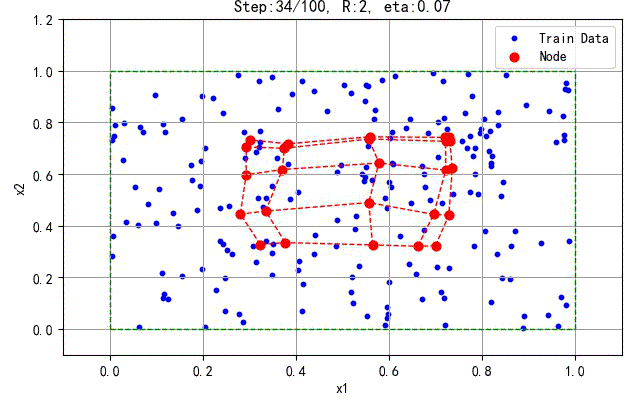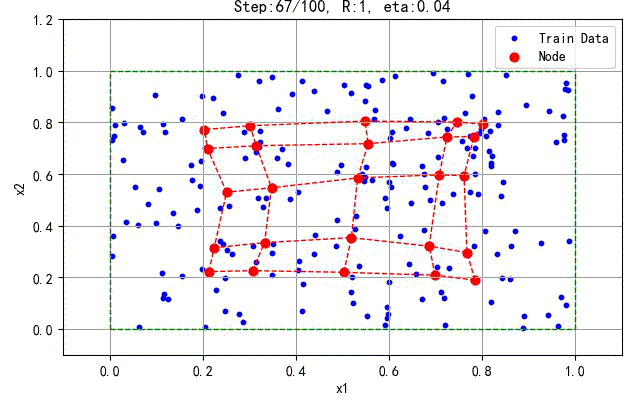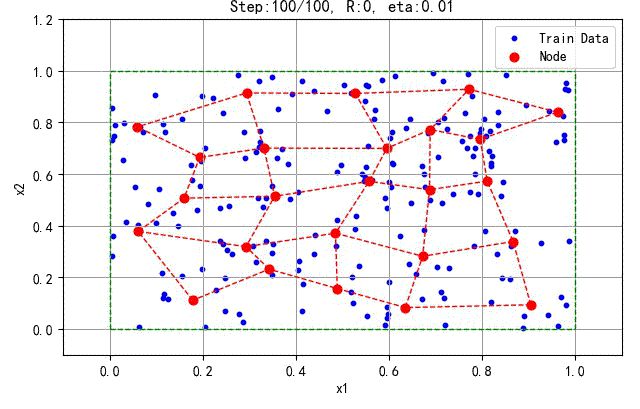
^{▲ 200个数据训练5×5的二维结构所产生的结果}

 

➤※ 作业中的程序

---

1.训练1D拓扑结构的程序

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# HW25.PY                      -- by Dr. ZhuoQing 2020-11-26
#
# Note:
#============================================================

from headm import *

#------------------------------------------------------------
def generate_data_triangle(num):
    """Generate the data point in triangle specifated in problems
    description.

    In: num-data point number.
    Out: Point array-2D.
    """

    pointdim = []

    for i in range(num):
        while True:
            x = random.uniform(0, 1)
            y = random.uniform(0, sqrt(3)/2)
            y_limit = sqrt(3) * (0.5 - abs(x-0.5))
            if y > y_limit:
                continue

            pointdim.append([x, y])
            break

    return array(pointdim)

def show_data(data, lineflag=0, title=''):
#    plt.clf()

    if lineflag ==0:
        plt.scatter(data[:,0], data[:,1], s=10, c='blue')
    else:
        plt.scatter(data[:,0], data[:,1], s=35, c='red')
        plt.plot(data[:,0], data[:,1], 'y-', linewidth=1)

    board_x = linspace(0, 1, 200)
    board_y = [sqrt(3)*(0.5-abs(x-0.5)) for x in board_x]
    plt.plot(board_x, board_y, 'c--', linewidth=1)
    plt.plot(board_x, zeros(len(board_x)), 'c--', linewidth=1)

    plt.xlabel("x1")
    plt.ylabel("x2")
    plt.axis([-0.05, 1.05, -0.05, .9])

    if len(title) > 0: plt.title(title)

    plt.grid(True)
    plt.tight_layout()
#    plt.draw()
#    plt.pause(.0001)

#------------------------------------------------------------
SAMPLE_NUM          = 300
NEURAL_NUM          = 100
x_data = generate_data_triangle(SAMPLE_NUM)
W = random.rand(NEURAL_NUM, x_data.shape[1])
W[:,1] *= sqrt(3)/2

#------------------------------------------------------------
def WTA2(x, w):
    """ Win-Take-All

    In: x-sample(x1,x2)
           w-net argument
    Ret: id-Win ID of w
    """
    dist = array([(x-ww).dot(x-ww) for ww in w])

    return list(where(dist==amin(dist)))[0][0]

#------------------------------------------------------------
def neighborid1(id, row, r):
    if r <= 0: return [id]

    iddim = []
    for i in range(-r,r+1):
        if id + i < 0:    continue
        if id + i >= row: continue

        iddim.append(id + i)

    return iddim

def compete1(x, w, eta, r):
    for xx in x:
        id = WTA2(xx, w)

        iddim = neighborid1(id, w.shape[0], r)

        for iidd in iddim:
            w[iidd] = w[iidd] + eta * (xx - w[iidd])

    return w

#------------------------------------------------------------
TRAIN_NUM       = 200
ETA_BEGIN       = 0.3
ETA_END         = 0.01
RATIO_BEGIN     = 10
RATIO_END        = 0

plt.draw()
plt.pause(.2)

pltgif = PlotGIF()
for i in range(TRAIN_NUM):

    eta = (ETA_BEGIN - ETA_END) * (TRAIN_NUM - i) / (TRAIN_NUM - 1) + ETA_END
    ratio = int((RATIO_BEGIN - RATIO_END) * (TRAIN_NUM - i) / (TRAIN_NUM - 1) + RATIO_END)

    W = compete1(x_data, W, eta, ratio)

    plt.clf()
    show_data(x_data, 0)
    show_data(W, 1, "Step:%d/%d, R:%d, eta:%4.2f"%(i+1, TRAIN_NUM, ratio, eta))
    plt.draw()
    plt.pause(0.001)
    pltgif.append(plt)

pltgif.save(r'd:\temp\1.gif')
plt.show()

#------------------------------------------------------------
#        END OF FILE : HW25.PY
#============================================================

2.训练2D拓扑结构而的SOFM程序

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# HW25_1.PY                      -- by Dr. ZhuoQing 2020-11-26
#
# Note:
#============================================================

from headm import *

#------------------------------------------------------------
def generate_data_rect(num):
    """Generate the data point in triangle specifated in problems
    description.

    In: num-data point number.
    Out: Point array-2D.
    """

    x_ = random.random(num)
    y_ = random.random(num)
    xy = vstack((x_, y_))
    return xy.T

def show_data(data):
    plt.scatter(data[:,0], data[:,1], s=10, c='blue', label='Train Data')
    plt.vlines(0, 0, 1, color='green', linewidth=1, linestyles='--')
    plt.vlines(1, 0, 1, color='green', linewidth=1, linestyles='--')
    plt.hlines(0, 0, 1, color='green', linewidth=1, linestyles='--')
    plt.hlines(1, 0, 1, color='green', linewidth=1, linestyles='--')
    plt.axis([-0.1, 1.1, -0.1, 1.2])
    plt.xlabel("x1")
    plt.ylabel("x2")
    plt.grid(True)

#------------------------------------------------------------
SAMPLE_NUM          = 200
NEURAL_NUM          = 5
x_data = generate_data_rect(SAMPLE_NUM)
W = stack((random.random((NEURAL_NUM, NEURAL_NUM)), random.random((NEURAL_NUM, NEURAL_NUM)))).T

def show_W(w):
    w_ = w.reshape(-1, 2)

    plt.scatter(w_[:,0], w_[:,1], s=40, c='red', label='Node')

    for ww in w:
        plt.plot(ww[:,0], ww[:,1], color='red', linewidth=1, linestyle='--')

    for ww in w.transpose((1,0,2)):
        plt.plot(ww[:,0], ww[:,1], color='red', linewidth=1, linestyle='--')

    plt.legend(loc="upper right")
    plt.tight_layout()

#------------------------------------------------------------
def WTA2(x, w):
    """ Win-Take-All

    In: x-sample(x1,x2)
           w-net argument
    Ret: id-Win ID of w
    """

    col = w.shape[1]
    dist = array([(x-ww).dot(x-ww) for ww in w.reshape(-1,2)])

    id = list(where(dist==amin(dist)))[0][0]
    idx = id % col
    idy = id // col
    return(idx, idy)

#------------------------------------------------------------
def neighborid1(id, row, col, r):
    if r <= 0: return [id]

    iddim = []

    idx = id[0]
    idy = id[1]

    for i in range(-r,r+1):
        if idy + i < 0:    continue
        if idy + i >= row: continue

        for j in range(-r,r+1):
            if idx + j < 0: continue
            if idx + j >= col: continue
            iddim.append((idx+j, idy+i))

    return iddim

def compete1(x, w, eta, r):
    for xx in x:
        id = WTA2(xx, w)

        iddim = neighborid1(id, w.shape[0], w.shape[1], r)

        for iidd in iddim:
            idx = iidd[0]
            idy = iidd[1]
            w[idy,idx] = w[idy,idx] + eta * (xx - w[idy,idx])

    return w

#------------------------------------------------------------
TRAIN_NUM       = 100
ETA_BEGIN       = 0.1
ETA_END         = 0.01
RATIO_BEGIN     = 3
RATIO_END        = 0

plt.draw()
plt.pause(.2)

pltgif = PlotGIF()
for i in range(TRAIN_NUM):

    eta = (ETA_BEGIN - ETA_END) * (TRAIN_NUM - i) / (TRAIN_NUM - 1) + ETA_END
    ratio = int((RATIO_BEGIN - RATIO_END) * (TRAIN_NUM - i) / (TRAIN_NUM - 1) + RATIO_END)

    W = compete1(x_data, W, eta, ratio)

    plt.clf()
    show_data(x_data)
    show_W(W)
    plt.title("Step:%d/%d, R:%d, eta:%4.2f"%(i+1, TRAIN_NUM, ratio, eta))
    plt.draw()
    plt.pause(0.001)
    pltgif.append(plt)

pltgif.save(r'd:\temp\1.gif')

printf('\a')
plt.show()

#------------------------------------------------------------
#        END OF FILE : HW25_1.PY
#============================================================