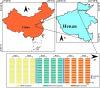
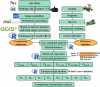
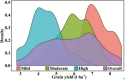
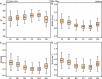
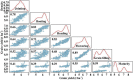
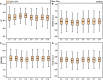
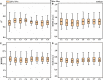
Crop breeding programs generally perform early field assessments of candidate selection based on primary traits such as grain yield (GY). The traditional methods of yield assessment are costly, inefficient, and considered a bottleneck in modern precision agriculture. Recent advances in an unmanned aerial vehicle (UAV) and development of sensors have opened a new avenue for data acquisition cost-effectively and rapidly. We evaluated UAV-based multispectral and thermal images for in-season GY prediction using 30 winter wheat genotypes under 3 water treatments. For this, multispectral vegetation indices (VIs) and normalized relative canopy temperature (NRCT) were calculated and selected by the gray relational analysis (GRA) at each growth stage, i.e., jointing, booting, heading, flowering, grain filling, and maturity to reduce the data dimension. The elastic net regression (ENR) was developed by using selected features as input variables for yield prediction, whereas the entropy weight fusion (EWF) method was used to combine the predicted GY values from multiple growth stages. In our results, the fusion of dual-sensor data showed high yield prediction accuracy [coefficient of determination (R ²) = 0.527-0.667] compared to using a single multispectral sensor (R ² = 0.130-0.461). Results showed that the grain filling stage was the optimal stage to predict GY with R ² = 0.667, root mean square error (RMSE) = 0.881 t ha^-1, relative root-mean-square error (RRMSE) = 15.2%, and mean absolute error (MAE) = 0.721 t ha^-1. The EWF model outperformed at all the individual growth stages with R ² varying from 0.677 to 0.729. The best prediction result (R ² = 0.729, RMSE = 0.831 t ha^-1, RRMSE = 14.3%, and MAE = 0.684 t ha^-1) was achieved through combining the predicted values of all growth stages. This study suggests that the fusion of UAV-based multispectral and thermal IR data within an ENR-EWF framework can provide a precise and robust prediction of wheat yield.