Simple discrete-time self-exciting models can describe complex dynamic processes: A case study of COVID-19 - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Apr 9;16(4):e0250015.
doi: 10.1371/journal.pone.0250015. eCollection 2021.

Simple discrete-time self-exciting models can describe complex dynamic processes: A case study of COVID-19

Raiha Browning  1   2 , Deborah Sulem  3 , Kerrie Mengersen  1   2 , Vincent Rivoirard  4 , Judith Rousseau  3   4
Affiliations

Simple discrete-time self-exciting models can describe complex dynamic processes: A case study of COVID-19

Raiha Browning et al. PLoS One. .

Abstract

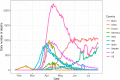
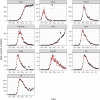
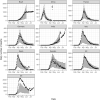
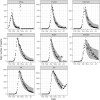
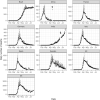
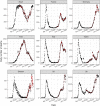
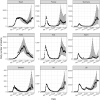
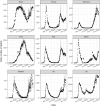
Hawkes processes are a form of self-exciting process that has been used in numerous applications, including neuroscience, seismology, and terrorism. While these self-exciting processes have a simple formulation, they can model incredibly complex phenomena. Traditionally Hawkes processes are a continuous-time process, however we enable these models to be applied to a wider range of problems by considering a discrete-time variant of Hawkes processes. We illustrate this through the novel coronavirus disease (COVID-19) as a substantive case study. While alternative models, such as compartmental and growth curve models, have been widely applied to the COVID-19 epidemic, the use of discrete-time Hawkes processes allows us to gain alternative insights. This paper evaluates the capability of discrete-time Hawkes processes by modelling daily mortality counts as distinct phases in the COVID-19 outbreak. We first consider the initial stage of exponential growth and the subsequent decline as preventative measures become effective. We then explore subsequent phases with more recent data. Various countries that have been adversely affected by the epidemic are considered, namely, Brazil, China, France, Germany, India, Italy, Spain, Sweden, the United Kingdom and the United States. These countries are all unique concerning the spread of the virus and their corresponding response measures. However, we find that this simple model is useful in accurately capturing the dynamics of the process, despite hidden interactions that are not directly modelled due to their complexity, and differences both within and between countries. The utility of this model is not confined to the current COVID-19 epidemic, rather this model could explain many other complex phenomena. It is of interest to have simple models that adequately describe these complex processes with unknown dynamics. As models become more complex, a simpler representation of the process can be desirable for the sake of parsimony.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Observed data.
Daily volume of deaths due to COVID-19 for the countries selected in this analysis.
Fig 2
Fig 2. Observed deaths versus estimated deaths.
The observed number of deaths (black dots) compared to the 95% posterior interval for the estimated expected number of events, i.e. λ(t) (solid red ribbon).
Fig 3
Fig 3. In-sample validation.
The observed number of deaths (black dots) compared to the 95% posterior predictive interval for the estimated expected number of events, i.e. λ(t) (grey ribbon).
Fig 4
Fig 4. In-sample validation, conditioned on data from the first phase.
The observed number of deaths (black dots) compared to the 95% posterior predictive interval for the estimated expected number of events, i.e. λ(t) (grey ribbon).
Fig 5
Fig 5. Out-of-sample validation.
The observed number of deaths (black dots) compared to the 95% posterior predictive interval for the estimated expected number of events, i.e. λ(t) using various training datasets (grey ribbons).
Fig 6
Fig 6. Observed deaths versus estimated deaths (subsequent analysis).
The observed number of deaths (black dots) compared to the 95% posterior interval for the estimated expected number of events, i.e. λ(t) (solid red ribbon), for the subsequent analysis.
Fig 7
Fig 7. In-sample validation for subsequent analysis, conditioned on data from the initial analysis.
The observed number of deaths (black dots) compared to the 95% posterior predictive interval for the estimated expected number of events, i.e. λ(t) (grey ribbon), for the subsequent analysis.
Fig 8
Fig 8. Out-of-sample validation (subsequent analysis).
The observed number of deaths (black dots) compared to the 95% posterior predictive interval for the estimated expected number of events, i.e. λ(t) using various training datasets (grey ribbons) for the subsequent analysis.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. World Health Organisation. Weekly Epidemiological Update for Coronavirus disease 2019 (COVID-19)—9 March 2021; 2021. https://www.who.int/docs/default-source/coronaviruse/situation-reports/2....
    1. Hellewell J, Abbott S, Gimma A, Bosse NI, Jarvis CI, Russell TW, et al.. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. The Lancet Global Health. 2020;8(4):e488–e496. 10.1016/S2214-109X(20)30074-7 - DOI - PMC - PubMed
    1. Plank MJ, Binny RN, Hendy SC, Lustig A, James A, Steyn N. A stochastic model for COVID-19 spread and the effects of Alert Level 4 in Aotearoa New Zealand. medRxiv. 2020;.
    1. Fowler JH, Hill SJ, Obradovich N, Levin R. The effect of stay-at-home orders on COVID-19 cases and fatalities in the United States. medRxiv. 2020;. - PMC - PubMed
    1. Peak CM, Kahn R, Grad YH, Childs LM, Li R, Lipsitch M, et al.. Individual quarantine versus active monitoring of contacts for the mitigation of COVID-19: a modelling study. The Lancet Infectious Diseases. 2020;20(9):1025–1033. 10.1016/S1473-3099(20)30361-3 - DOI - PMC - PubMed

Grants and funding

The author(s) received no specific funding for this work.