Generalized Linear Quadratic Control for a Full Tracking Problem in Aviation - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 May 22;20(10):2955.
doi: 10.3390/s20102955.

Generalized Linear Quadratic Control for a Full Tracking Problem in Aviation

Franciszek Dul  1 , Piotr Lichota  1 , Artur Rusowicz  2
Affiliations

Generalized Linear Quadratic Control for a Full Tracking Problem in Aviation

Franciszek Dul et al. Sensors (Basel). .

Abstract

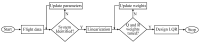
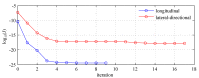
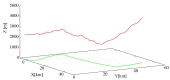
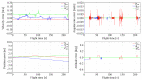
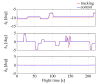
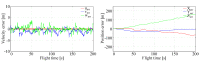
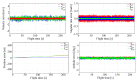
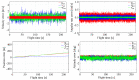
In this paper, the full tracking problem in aircraft system identification and control is presented. Time domain output error method with maximum likelihood principle was used to perform system identification. The linear quadratic regulator (LQR)-based approach has been used for solving aviation full tracking problems in aviation. It has been shown that the generalized nonlinear LQR control is able to handle such problems even in case of inaccurate measurements and in the presence of moderate disturbances provided that the model of an aircraft is properly identified.

Keywords: LQR; aviation; control; system identification; trajectory tracking.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
LQR design flowchart.
Figure 2
Figure 2
Aircraft model.
Figure 3
Figure 3
Cost function.
Figure 4
Figure 4
Exemplary trajectory.
Figure 5
Figure 5
Full tracking errors, quiet atmosphere.
Figure 6
Figure 6
Controls errors.
Figure 7
Figure 7
Full tracking in turbulent conditions.
Figure 8
Figure 8
Full tracking in constant wind presence.
Figure 9
Figure 9
Full tracking errors—flight parameters disturbed by 1 unit (Case 1).
Figure 10
Figure 10
Full tracking errors—flight parameters disturbed by 2 units (Case 2).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Al-Hiddabi S.A., McClamroch N.H. Aggressive Longitudinal Aircraft Path Tracking Using Nonlinear Control. Asian J. Control. 2001;3:280–288. doi: 10.1111/j.1934-6093.2001.tb00068.x. - DOI
    1. Sun H., Yang Z., Zeng J. New Tracking-Control Strategy for Airbreathing Hypersonic Vehicles. J. Guid. Control. Dyn. 2013;36:846–859. doi: 10.2514/1.57739. - DOI
    1. Zhao Y., Tsiotras P. Analysis of Energy-Optimal Aircraft Landing Operation Trajectories. J. Guid. Control Dyn. 2013;36:833–845. doi: 10.2514/1.57779. - DOI
    1. Schmitt L., Fichter W. Continuous Singularity Free Approach to the Three-Dimensional Bearings-Only Tracking Problem. J. Guid. Control. Dyn. 2016;39:2673–2682. doi: 10.2514/1.G000362. - DOI
    1. Xia D., Cheng L., Yao Y. A Robust Inner and Outer Loop Control Method for Trajectory Tracking of a Quadrotor. Sensors. 2017;17:2147. doi: 10.3390/s17092147. - DOI - PMC - PubMed

LinkOut - more resources