Morphology of travel routes and the organization of cities

doi:10.1038/s41467-017-02374-7

. 2017 Dec 20;8(1):2229.

doi: 10.1038/s41467-017-02374-7.

Morphology of travel routes and the organization of cities

Minjin Lee¹, Hugo Barbosa², Hyejin Youn^{3

4

5

6}, Petter Holme⁷, Gourab Ghoshal^{8

9}

Affiliations

¹ Department of Energy Science, Sungkyunkwan University, Suwon, 16419, Korea.
² Department of Physics and Astronomy, University of Rochester, Rochester, NY, 14627, USA.
³ Kellogg School of Management at Northwestern University, Evanston, IL, 60208, USA.
⁴ Santa Fe Institute, 1399 Hyde Park Road, Santa Fe, NM, 87501, USA.
⁵ London Mathematical Lab, London, WC2N 6DF, UK.
⁶ Northwestern Institute on Complex Systems, Northwestern University, Evanston, IL, 60208, USA.
⁷ Institute of Innovative Research, Tokyo Institute of Technology, Nagatsuta-cho 4259, Midori-ku, Yokohama, Kanagawa, 226-8503, Japan.
⁸ Department of Physics and Astronomy, University of Rochester, Rochester, NY, 14627, USA. gghoshal@pas.rochester.edu.
⁹ Goergen Institute for Data Science, University of Rochester, Rochester, NY, 14627, USA. gghoshal@pas.rochester.edu.

PMID: 29263392
PMCID: PMC5738436
DOI: 10.1038/s41467-017-02374-7

Morphology of travel routes and the organization of cities

Minjin Lee et al. Nat Commun. 2017.

. 2017 Dec 20;8(1):2229.

doi: 10.1038/s41467-017-02374-7.

Authors

Minjin Lee¹, Hugo Barbosa², Hyejin Youn^{3

4

5

6}, Petter Holme⁷, Gourab Ghoshal^{8

9}

Affiliations

¹ Department of Energy Science, Sungkyunkwan University, Suwon, 16419, Korea.
² Department of Physics and Astronomy, University of Rochester, Rochester, NY, 14627, USA.
³ Kellogg School of Management at Northwestern University, Evanston, IL, 60208, USA.
⁴ Santa Fe Institute, 1399 Hyde Park Road, Santa Fe, NM, 87501, USA.
⁵ London Mathematical Lab, London, WC2N 6DF, UK.
⁶ Northwestern Institute on Complex Systems, Northwestern University, Evanston, IL, 60208, USA.
⁷ Institute of Innovative Research, Tokyo Institute of Technology, Nagatsuta-cho 4259, Midori-ku, Yokohama, Kanagawa, 226-8503, Japan.
⁸ Department of Physics and Astronomy, University of Rochester, Rochester, NY, 14627, USA. gghoshal@pas.rochester.edu.
⁹ Goergen Institute for Data Science, University of Rochester, Rochester, NY, 14627, USA. gghoshal@pas.rochester.edu.

PMID: 29263392
PMCID: PMC5738436
DOI: 10.1038/s41467-017-02374-7

Abstract

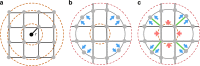
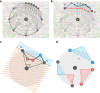
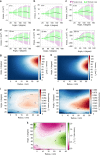
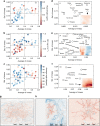
The city is a complex system that evolves through its inherent social and economic interactions. Mediating the movements of people and resources, urban street networks offer a spatial footprint of these activities. Of particular interest is the interplay between street structure and its functional usage. Here, we study the shape of 472,040 spatiotemporally optimized travel routes in the 92 most populated cities in the world, finding that their collective morphology exhibits a directional bias influenced by the attractive (or repulsive) forces resulting from congestion, accessibility, and travel demand. To capture this, we develop a simple geometric measure, inness, that maps this force field. In particular, cities with common inness patterns cluster together in groups that are correlated with their putative stage of urban development as measured by a series of socio-economic and infrastructural indicators, suggesting a strong connection between urban development, increasing physical connectivity, and diversity of road hierarchies.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no competing financial interests.

Figures

**Fig. 1**
Biasing forces found in urban morphology. Three schematic urban street arrangements share similar topological structure, but different geometric layouts resulting in varying dynamics. a A grid structure where the shortest paths between points at the same radius show no directional bias. b Repulsive forces relative to the origin (marked in blue) emerge as we break the grid symmetry by relocating the four outer points on the inner equidistant ring line. Paths lying on this ring now have the shortest paths that traverse the periphery and avoid the center. c Further perturbing the topology by increasing connectivity to the center (marked as four green lines) now leads to shortest paths that go through the center as if an attractive force is present (marked in red)

**Fig. 2**
Data sampling and definition of inness I. a Thirty-six origin–destination (OD) pairs (spaced out at intervals of 10°) are assigned along the circumference of circles at a distance of 2, 5, 10, 15, 20, and 30 km from the city center C. b For each OD pair, we query the Open Source Map API and collect the shortest routes (red) and the fastest routes (blue) (shown here for a representative OD pair in Paris). c A typical OD pair with the straight line connecting them representing the geodesic distance s; r is the radial distance from the center and θ is the angular separation relative to the center. We define the inness (I) to be the difference between the inner travel area (polygon delineated by red inner point and straight line) and the outer travel area (polygon delineated by blue outer point and straight line). d Three possible route configurations between multiple OD pairs. One with an exclusively outer travel area (blue), one with an exclusively inner travel area (red), and one where there is some combination of both

**Fig. 3**
The average inness across 92 cities. The average and standard deviation of I as a function of θ shown for multiple radii r measured from the city center; a 2 km, b 5 km, c 10 km, d 15 km, e 20 km, and f 30 km. The curve for the shortest route is shown in green and the fastest route in purple. The density plot of $⟨I⟩$ in function of r and θ for the shortest routes g and fastest routes h. The normalized or dimensionless inness $⟨Î⟩ = ⟨I ∕ s^{2}⟩$ for the shortest i and fastest routes j. k Ratio of the normalized inness of fastest ${⟨Î⟩}_{f}$ and shortest routes ${⟨Î⟩}_{s}$

**Fig. 4**
The statistics and spatial distribution of the inness for individual cities. The standard deviation plotted in function of average inness for each city. The cities are divided into three groups by their value of average and standard deviation of inness; Low–Low (LL), Low–High (LH), High–High (HH). The color of the points indicates the road length a, the level of geographical constraint (GC) b, and a measure of peripheral connectivity c. We enlarge three zones marked LL, LH, and HH and label the cities explicitly in d–f as well as display in inset $Î$ , for representative cities in each region (Berlin, Mumbai, Kolkata). In g, h, and i we plot the spatial distribution of $Î$ projected on to the physical maps for the three representative cities. The color of street intersections corresponds to the average $Î$ of all routes passing through the intersection, with values in the interval $- 0.3 \leq Î \leq 0.3$ and ranges from blue to red with increasing $Î$

**Fig. 5**
Difference between shortest routes and fastest routes. Shortest routes a and fastest routes b for Berlin. Shortest routes c and fastest routes d for Mumbai. The insets show the density plots of $Î$ with the same range as in Fig. 4. e Pearson correlation coefficient ρ between the inness patterns of shortest and fastest routes for each city. Cities are categorized into three groups (marked by vertical dashed lines) based on a K-means clustering and Jenks natural breaks optimization, conditioned on their level of correlation ρ. The names of cities in each type are listed in Supplementary Note 6. Three socio-economic indices, Productivity index f, Infrastructure development index g, and GDP per capita h, are plotted as a function of ρ showing a clear monotonically decreasing trend. Points are averages over cities binned in intervals of 0.2, and bars represent the standard error

See this image and copyright information in PMC

Cited by

The temporal network of mobile phone users in Changchun Municipality, Northeast China.
Du Z, Yang Y, Gao C, Huang L, Huang Q, Bai Y. Du Z, et al. Sci Data. 2018 Oct 30;5:180228. doi: 10.1038/sdata.2018.228. Sci Data. 2018. PMID: 30375989 Free PMC article.
Characterizing network circuity among heterogeneous urban amenities.
Poudyal B, Ghoshal G, Kirkley A. Poudyal B, et al. J R Soc Interface. 2023 Nov;20(208):20230296. doi: 10.1098/rsif.2023.0296. Epub 2023 Nov 1. J R Soc Interface. 2023. PMID: 37907093 Free PMC article.
From the betweenness centrality in street networks to structural invariants in random planar graphs.
Kirkley A, Barbosa H, Barthelemy M, Ghoshal G. Kirkley A, et al. Nat Commun. 2018 Jun 27;9(1):2501. doi: 10.1038/s41467-018-04978-z. Nat Commun. 2018. PMID: 29950619 Free PMC article.
A unified spatial multigraph analysis for public transport performance.
Wang Y, Zhu D, Yin G, Huang Z, Liu Y. Wang Y, et al. Sci Rep. 2020 Jun 12;10(1):9573. doi: 10.1038/s41598-020-65175-x. Sci Rep. 2020. PMID: 32532999 Free PMC article.
Data-driven strategies for optimal bicycle network growth.
Natera Orozco LG, Battiston F, Iñiguez G, Szell M. Natera Orozco LG, et al. R Soc Open Sci. 2020 Dec 16;7(12):201130. doi: 10.1098/rsos.201130. eCollection 2020 Dec. R Soc Open Sci. 2020. PMID: 33489269 Free PMC article.

See all "Cited by" articles

References

1. Bettencourt L, West G. A unified theory of urban living. Nature. 2010;467:912–913. doi: 10.1038/467912a. - DOI - PubMed
1. Pan W, Ghoshal G, Krumme C, Cebrian M, Pentland A. Urban characteristics attributable to density-driven tie formation. Nat. Commun. 2013;4:1–7. - PubMed
1. Batty M. Building a science of cities. Cities. 2012;29:S9–S16. doi: 10.1016/j.cities.2011.11.008. - DOI
1. Sim A, Yaliraki SN, Barahona M, Stumpf MPH. Great cities look small. J. R. Soc. Interface. 2015;12:20150315. doi: 10.1098/rsif.2015.0315. - DOI - PMC - PubMed
1. Youn H, Gastner MT, Jeong H. Price of anarchy in transportation networks: efficiency and optimality control. Phys. Rev. Lett. 2008;101:128701. doi: 10.1103/PhysRevLett.101.128701. - DOI - PubMed

Publication types

Actions

LinkOut - more resources

Full Text Sources
Other Literature Sources
- scite Smart Citations

[1] Bettencourt L, West G. A unified theory of urban living. Nature. 2010;467:912–913. doi: 10.1038/467912a. - DOI - PubMed

[2] Bettencourt L, West G. A unified theory of urban living. Nature. 2010;467:912–913. doi: 10.1038/467912a. - DOI - PubMed

[3] Pan W, Ghoshal G, Krumme C, Cebrian M, Pentland A. Urban characteristics attributable to density-driven tie formation. Nat. Commun. 2013;4:1–7. - PubMed

[4] Pan W, Ghoshal G, Krumme C, Cebrian M, Pentland A. Urban characteristics attributable to density-driven tie formation. Nat. Commun. 2013;4:1–7. - PubMed

[5] Batty M. Building a science of cities. Cities. 2012;29:S9–S16. doi: 10.1016/j.cities.2011.11.008. - DOI

[6] Batty M. Building a science of cities. Cities. 2012;29:S9–S16. doi: 10.1016/j.cities.2011.11.008. - DOI

[7] Sim A, Yaliraki SN, Barahona M, Stumpf MPH. Great cities look small. J. R. Soc. Interface. 2015;12:20150315. doi: 10.1098/rsif.2015.0315. - DOI - PMC - PubMed

[8] Sim A, Yaliraki SN, Barahona M, Stumpf MPH. Great cities look small. J. R. Soc. Interface. 2015;12:20150315. doi: 10.1098/rsif.2015.0315. - DOI - PMC - PubMed

[9] Youn H, Gastner MT, Jeong H. Price of anarchy in transportation networks: efficiency and optimality control. Phys. Rev. Lett. 2008;101:128701. doi: 10.1103/PhysRevLett.101.128701. - DOI - PubMed

[10] Youn H, Gastner MT, Jeong H. Price of anarchy in transportation networks: efficiency and optimality control. Phys. Rev. Lett. 2008;101:128701. doi: 10.1103/PhysRevLett.101.128701. - DOI - PubMed

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Morphology of travel routes and the organization of cities

Affiliations

Morphology of travel routes and the organization of cities

Authors

Affiliations

Abstract

Conflict of interest statement

Figures

Similar articles

Cited by

References

Publication types

LinkOut - more resources

Full Text Sources

Other Literature Sources