Baseline Signal Reconstruction for Temperature Compensation in Lamb Wave-Based Damage Detection - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2016 Aug 11;16(8):1273.
doi: 10.3390/s16081273.

Baseline Signal Reconstruction for Temperature Compensation in Lamb Wave-Based Damage Detection

Guoqiang Liu  1 , Yingchun Xiao  2 , Hua Zhang  3 , Gexue Ren  4
Affiliations

Baseline Signal Reconstruction for Temperature Compensation in Lamb Wave-Based Damage Detection

Guoqiang Liu et al. Sensors (Basel). .

Abstract

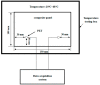
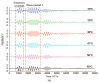
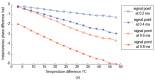
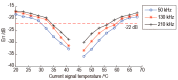
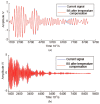
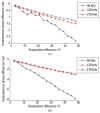
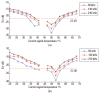
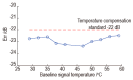
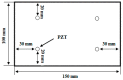
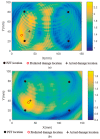
Temperature variations have significant effects on propagation of Lamb wave and therefore can severely limit the damage detection for Lamb wave. In order to mitigate the temperature effect, a temperature compensation method based on baseline signal reconstruction is developed for Lamb wave-based damage detection. The method is a reconstruction of a baseline signal at the temperature of current signal. In other words, it compensates the baseline signal to the temperature of current signal. The Hilbert transform is used to compensate the phase of baseline signal. The Orthogonal matching pursuit (OMP) is used to compensate the amplitude of baseline signal. Experiments were conducted on two composite panels to validate the effectiveness of the proposed method. Results show that the proposed method could effectively work for temperature intervals of at least 18 °C with the baseline signal temperature as the center, and can be applied to the actual damage detection.

Keywords: Hilbert transform; damage detection; lamb waves; orthogonal matching pursuit; temperature compensation.

PubMed Disclaimer

Figures

Figure 1
Figure 1
The flowchart of the proposed temperature compensation method. BS: baseline signal, RS: reference signal, CS: current signal.
Figure 2
Figure 2
The schematic diagram of the PZT positions on the specimen used for temperature compensation validation without damage.
Figure 3
Figure 3
The experimental setup. (a) Specimen of composite panel; (b) Experiment test system.
Figure 4
Figure 4
Signals with frequency 50 kHz at different temperatures. (a) A waterfall plot of the whole waveform; (b) Wave packet 1.
Figure 4
Figure 4
Signals with frequency 50 kHz at different temperatures. (a) A waterfall plot of the whole waveform; (b) Wave packet 1.
Figure 5
Figure 5
The relationships between the instantaneous phase difference and the temperature difference: (a) Signal with frequency 50 kHz; (b) Signal with frequency 130 kHz; (c) Signal with frequency 210 kHz.
Figure 5
Figure 5
The relationships between the instantaneous phase difference and the temperature difference: (a) Signal with frequency 50 kHz; (b) Signal with frequency 130 kHz; (c) Signal with frequency 210 kHz.
Figure 6
Figure 6
The temperature compensation results using 44 °C baseline signal and 47 °C reference signal.
Figure 7
Figure 7
The comparison of 53 °C current signal and the temperature compensation signal of 44 °C baseline signal at two frequencies: (a) Signal with frequency 50 kHz; (b) Signal with frequency 190 kHz.
Figure 8
Figure 8
The comparison of the relationship between the instantaneous phase difference and the temperature difference for same signal point at different frequency: (a) Signal point at 0.2 ms; (b) Signal point at 0.4 ms.
Figure 9
Figure 9
The temperature compensation results using 44 °C baseline signal and 50 °C, 53 °C reference signals: (a) The result using 50 °C reference signal; (b) The result using 53 °C reference signal.
Figure 10
Figure 10
The worst temperature compensation results for each baseline signal for temperature interval 18 °C with the baseline signal temperature as the center.
Figure 11
Figure 11
The schematic diagram of the PZT positions on the specimen used for damage detection validation.
Figure 12
Figure 12
Damage imaging results: (a) Imaging result without temperature compensation; (b) Imaging result with temperature compensation.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Hu N., Shimomukai T., Fukunaga H., Su Z.Q. Damage identification of metallic structures using A0 mode of Lamb wave. Struct. Health Monit. 2008;7:271–285.
    1. Mujica L.E., Vehi J., Ruiz M., Verleysen M., Staszewski W., Worden K. Multivariate statistics process control for dimensionality reduction in structural assessment. Mech. Syst. Signal Process. 2008;22:155–171. doi: 10.1016/j.ymssp.2007.05.001. - DOI
    1. Stolze F., Staszewski W.J., Manson G., Worden K. Fatigue crack detection in a multi-riveted strap joint aluminium panel. Proc. SPIE. 2009;7295 doi: 10.1117/12.815738. - DOI - PMC - PubMed
    1. Levine R.M., Michaels J.E. Model-based imaging of damage with Lamb waves via sparse reconstruction. J. Acoust. Soc. Am. 2013;133:1525–1534. doi: 10.1121/1.4788984. - DOI - PubMed
    1. Sharif-Khodaei Z., Aliabadi M.H. Assessment of delay-and-sum algorithms for damage detection in aluminium and composite plates. Smart Mater. Struct. 2014;23:628–634. doi: 10.1088/0964-1726/23/7/075007. - DOI

LinkOut - more resources