Homeostatic role of heterosynaptic plasticity: models and experiments - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2015 Jul 13:9:89.
doi: 10.3389/fncom.2015.00089. eCollection 2015.

Homeostatic role of heterosynaptic plasticity: models and experiments

Marina Chistiakova  1 , Nicholas M Bannon  1 , Jen-Yung Chen  2 , Maxim Bazhenov  2 , Maxim Volgushev  1
Affiliations
Review

Homeostatic role of heterosynaptic plasticity: models and experiments

Marina Chistiakova et al. Front Comput Neurosci. .

Abstract

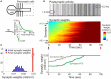
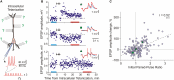
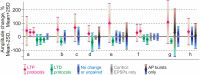
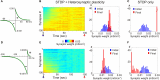
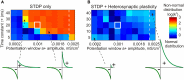
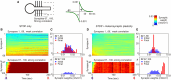
Homosynaptic Hebbian-type plasticity provides a cellular mechanism of learning and refinement of connectivity during development in a variety of biological systems. In this review we argue that a complimentary form of plasticity-heterosynaptic plasticity-represents a necessary cellular component for homeostatic regulation of synaptic weights and neuronal activity. The required properties of a homeostatic mechanism which acutely constrains the runaway dynamics imposed by Hebbian associative plasticity have been well-articulated by theoretical and modeling studies. Such mechanism(s) should robustly support the stability of operation of neuronal networks and synaptic competition, include changes at non-active synapses, and operate on a similar time scale to Hebbian-type plasticity. The experimentally observed properties of heterosynaptic plasticity have introduced it as a strong candidate to fulfill this homeostatic role. Subsequent modeling studies which incorporate heterosynaptic plasticity into model neurons with Hebbian synapses (utilizing an STDP learning rule) have confirmed its ability to robustly provide stability and competition. In contrast, properties of homeostatic synaptic scaling, which is triggered by extreme and long lasting (hours and days) changes of neuronal activity, do not fit two crucial requirements for a hypothetical homeostatic mechanism needed to provide stability of operation in the face of on-going synaptic changes driven by Hebbian-type learning rules. Both the trigger and the time scale of homeostatic synaptic scaling are fundamentally different from those of the Hebbian-type plasticity. We conclude that heterosynaptic plasticity, which is triggered by the same episodes of strong postsynaptic activity and operates on the same time scale as Hebbian-type associative plasticity, is ideally suited to serve a homeostatic role during on-going synaptic plasticity.

Keywords: Hebbian plasticity; STDP; heterosynaptic plasticity; homeostasis; homosynaptic plasticity; runaway dynamics; synaptic plasticity.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Multiple forms of plasticity at cortical synapses. (A) Homosynaptic and heterosynaptic plasticity. Left: In CA1 region of the hippocampus, LTP at Schaffer collateral inputs (red) induced by afferent tetanization is accompanied by heterosynaptic LTD at commissural inputs to basal dendrites (Lynch et al., 1977). Right: Mexican-hat profile of plasticity in hippocampus (White et al., 1990) and amygdala (Royer and Paré, 2003). (B) Heterosynaptic plasticity can be induced by purely postsynaptic protocol, intracellular tetanization—bursts of spikes evoked by depolarizing pulses without presynaptic stimulation in hippocampus (Kuhnt et al., 1994) and neocortex (Volgushev et al., 1994, 1997). Question marks denote that individual synapses may undergo LTP or LTD or do not change after the same induction. (C) Homeostatic synaptic scaling: prolonged (hours/days) changes of activity lead to compensatory up-scaling or down-scaling of synaptic weights (Turrigiano et al., 1998).
Figure 2
Figure 2
Synaptic activity produced by weakly correlated inputs leads to runaway dynamics of synaptic weights in a model with symmetrical STDP mechanism. (A) A scheme of a model neuron and STDP learning rule. The model neuron consisted of axosomatic and dendritic compartments, receiving 100 synaptic inputs from 100 presynaptic neurons. Each presynaptic neuron fired action potentials at ~1 Hz, with Poisson distributed interspike intervals. In simulations shown in this figure, firing of input neurons was mildly correlated (averaged cross-correlation 0.348 + −0.05). The STDP learning rule had symmetrical potentiation and depression windows (τ+ = τ− = 20 ms; a+ = a− = 10−3 mS/cm2). (B) Membrane potential trace of the model neuron (top); changes of the weights of 100 synapses (middle), color coded, with synapses sorted by their synaptic weights at the beginning of experiment; and changes of the weights of synapses #10 and #90 (bottom). In this model with symmetrical STDP learning rule synaptic inputs expressed runaway dynamics, and all inputs were potentiated to the maximum by the end of the simulation. (C) Distributions of synaptic weights at the beginning (blue, at 20 ms) and at the end (red, at 100 s) of simulation experiment shown in (B). Note runaway dynamics of synaptic weights leading to their saturation at the extreme value (0.03 mS/cm2; red bar length is out of scale) and associated increase of the firing rate of postsynaptic neuron from 1.8 to 6.3 Hz. (Modified, with permission from Chen et al., 2013).
Figure 3
Figure 3
Synaptic activity produced by weakly correlated inputs leads to runaway dynamics of synaptic weights in a model with negatively biased STDP mechanism. (A) A scheme of the model neuron and STDP learning rule. The STDP learning rule with negative bias (τ+ = 5 ms, a+ = 0. 5 × 10−3 mS/cm2, τ− = 40 ms, a− = 1.5 × 10−3 mS/cm2). (B) Membrane potential trace of the model neuron (top) receiving input from presynaptic neurons firing at an average rate of 1 Hz during first 50 s of simulation, 2 Hz during 50–100 s and 3 Hz during 100–150 s, as indicated; changes of the weights of 100 synapses (middle), color coded, with synapses sorted by their synaptic weights at the beginning of experiment; and changes of the weights of synapses #10, #50, and #90 (bottom). In this model with negatively biased STDP learning rule synaptic inputs expressed runaway dynamics toward the minimum value. (C) Distributions of synaptic weights at the beginning (blue, at 20 ms) and at the end (red, at 150 s) of simulation experiment shown in (B). Note runaway dynamics of synaptic weights leading to saturation at zero of about 40% of synapses, and associated dramatic decrease of postsynaptic firing rate despite a 3-fold increase of presynaptic firing. (Modified, with permission from Chen et al., 2013).
Figure 4
Figure 4
Long-term synaptic plasticity induced by intracellular tetanization. (A) A scheme of an intracellular tetanization experiment. Bursts of short depolarizing pulses (5 pulses at 100 Hz; 10 bursts at 1 Hz, 3 trains of 10 bursts) were applied through the recording electrode without presynaptic stimulation to induce bursts of action potentials. Synaptic responses were recorded before and after the intracellular tetanization. Because no inputs were stimulated during the induction, plasticity at all synapses can be considered heterosynaptic. (B) Examples of inputs that underwent potentiation (top), depression (middle), or did not change (bottom) after intracellular tetanization in pyramidal neurons from slices of rat visual cortex. Time courses of amplitudes of EPSPs evoked by the first pulse in a paired-pulse paradigm. The timing of intracellular tetanization is indicated by the arrows above each plot. Insets show averaged responses to paired pulse stimuli before and after intracellular tetanization, from color-coded time intervals. In this example, LTP and LTD were induced simultaneously at two inputs to the same neuron (top and middle). Note that input resistance of neurons measured by responses to small hyperpolarizing pulses applied before synaptic stimuli remained unchanged. (C) Correlation between changes of EPSP amplitude after intracellular tetanization and initial paired-pulse ratio. Data for N = 136 inputs to pyramidal neurons in slices of visual cortex (N = 60 inputs) and auditory cortex (N = 76 inputs). Green symbols (star, square, and triangle) refer to the example inputs from (B). (Modified, with permission, from Chen et al., 2013).
Figure 5
Figure 5
Comparison of reported changes of response amplitude at inputs that were active during the induction (homosynaptic, input-specific) and those not active during the induction (heterosynaptic). The plot shows results of 36 experimental series (bars) from eight papers (groups of bars) on pairing-induced long-term plasticity (STDP), in which the mean amplitude changes were reported together with the SD (or SEM) and number of observations. Each bar shows an average (diamond symbol) change of EPSP amplitude after pairing procedure ±2 SD. This range includes 95% of normally distributed values. Magenta: changes after LTP protocols (post after pre). Green: changes after LTD protocols (pre after post). Blue: range of EPSP amplitudes after protocols that did not lead to significant changes of the averaged response (such as interval between pre and post spikes outside plasticity windows). Gray: range of EPSP amplitudes after only presynaptic stimulation without postsynaptic spikes. Black, bars from cyan to pink (in d,e,h): range of EPSP amplitudes after bursts of postsynaptic spikes only, without presynaptic stimulation. Data for excitatory inputs to L2/3 or L5 pyramidal neurons from somatosensory, visual or auditory cortex, from the following papers: Feldman (2000) (a); Sjöström et al. (2001) (b); Watt et al. (2004) (c); Birtoli and Ulrich (2004) (d); Nevian and Sakmann (2006) (e); Letzkus et al. (2006) (f); Hardingham et al. (2007) (g); Chistiakova et al. (2014) (h). Results from Hardingham et al. (2007) (g) present the LTP and LTD data selected by the direction of the change. The third bar in this group shows LTP and LTD data pooled together. Details of experimental protocols can be found in original papers. (Modified, with permission, from Chistiakova et al., 2014).
Figure 6
Figure 6
Heterosynaptic plasticity prevents runaway dynamics produced by positively and negatively biased STDP. (A,D) STDP rules. STDP learning rule with symmetrical potentiation and depression windows (A, τ+ = τ− = 20 ms; a+ = a− = 10−3 mS/cm2), and with negative bias (D, τ+ = 5 ms, a+ = 0.5 × 10−3 mS/cm2, τ− = 40 ms, a− = 1.5 × 10−3 mS/cm2). (B,E) Heterosynaptic plasticity prevents runaway dynamics of synaptic weights. Same models as in Figures 2, 3 but with the mechanism for heterosynaptic plasticity as described in Chen et al. (2013). Note that in both models, with symmetrical (B) and negatively-biased (E) STDP rules, synaptic weights are not saturated, but remain normally distributed within the operation rage. (C,F) For comparison, distributions of synaptic weights in STDP only models from Figures 2, 3, expressing runaway dynamics are shown. (Modified, with permission, from Chen et al., 2013).
Figure 7
Figure 7
STDP only model fails to prevent runaway dynamics of synaptic weights in broad range of STDP rules (A). Heterosynaptic plasticity makes a broad range of STDP parameters compatible with stable operation of neurons (B). Each box in the grids shows the D'Agostino-Pearson's K2-test for normality of synaptic weight distribution after 100 s of simulations with different STDP potentiation windows, with a+ and τ+ as indicated on the X and Y axes. White square indicates symmetrical STDP learning rule. Synaptic weight distributions with high K2-test values (>50) indicating deviation from normality, typically contain most of the weights saturated at maximal or minimal values. Note that in simulations with the STDP only model (A), only few STDP rules, with strong bias toward depression, did not lead to runaway dynamics. Most STDP rules, including examples shown in the bottom, led to runaway dynamics of synaptic weights. In contrast, the model with STDP and heterosynaptic plasticity (B) did not express runaway dynamics over the whole range of tested STDP rules, including those extremely unbalanced (insets, bottom). (Modified, with permission, from Chen et al., 2013).
Figure 8
Figure 8
Segregation of synaptic weights of strongly vs. weakly correlated inputs in STDP models with and without heterosynaptic plasticity. (A) A model neuron received input from N = 100 presynaptic neurons firing at average frequency of 1 Hz. Spike trains of 66 presynaptic neurons (inputs # 1–66) were weakly correlated (averaged cross-correlation 0.34 + 0.02), spike trains of 34 presynaptic neurons (inputs # 67–100) were strongly correlated (averaged cross-correlation 0.61 + 0.05). Symmetrical STDP rule was used in the simulations, with τ+ = τ− = 20 ms; a+ = a− = 10−3 mS/cm2. (B,D) Dynamics of synaptic weights of weakly correlated inputs (synapses # 1…66) and strongly correlated inputs (synapses # 67…100) in the model with STDP only (B) and the model with STDP and heterosynaptic plasticity (D). (C,E) Distributions of synaptic weights at the beginning (blue bars) and at the end (red) of simulations from (B,D), respectively. Note runaway dynamics of synaptic weights and their saturation at the highest value (0.03 mS/cm2) for the group of strongly correlated inputs in STDP-only simulation. (Modified, with permission, from Chen et al., 2013).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Abbott L. F., Nelson S. B. (2000). Synaptic plasticity: taming the beast. Nat. Neurosci. 3, 1178–1183. 10.1038/81453 - DOI - PubMed
    1. Abbott L. F., Regehr W. G. (2004). Synaptic computation. Nature 431, 796–803. 10.1038/nature03010 - DOI - PubMed
    1. Abbott L. F., Varela J. A., Sen K., Nelson S. B. (1997). Synaptic depression and cortical gain control. Science 275, 220–224. 10.1126/science.275.5297.221 - DOI - PubMed
    1. Abraham W. C., Bear M. F. (1996). Metaplasticity: the plasticity of synaptic plasticity. Trends Neurosci. 19, 126–130. 10.1016/S0166-2236(96)80018-X - DOI - PubMed
    1. Aitkin L. M., Anderson D. J., Brugge J. F. (1970). Tonotopic organization and discharge characteristics of single neurons in nuclei of the lateral lemniscus of the cat. J. Neurophysiol. 33, 421–440. - PubMed

LinkOut - more resources