Mathematical model of adult stem cell regeneration with cross-talk between genetic and epigenetic regulation
- PMID: 24501127
- PMCID: PMC3956188
- DOI: 10.1073/pnas.1324267111
Mathematical model of adult stem cell regeneration with cross-talk between genetic and epigenetic regulation
Abstract
Adult stem cells, which exist throughout the body, multiply by cell division to replenish dying cells or to promote regeneration to repair damaged tissues. To perform these functions during the lifetime of organs or tissues, stem cells need to maintain their populations in a faithful distribution of their epigenetic states, which are susceptible to stochastic fluctuations during each cell division, unexpected injury, and potential genetic mutations that occur during many cell divisions. However, it remains unclear how the three processes of differentiation, proliferation, and apoptosis in regulating stem cells collectively manage these challenging tasks. Here, without considering molecular details, we propose a genetic optimal control model for adult stem cell regeneration that includes the three fundamental processes, along with cell division and adaptation based on differential fitnesses of phenotypes. In the model, stem cells with a distribution of epigenetic states are required to maximize expected performance after each cell division. We show that heterogeneous proliferation that depends on the epigenetic states of stem cells can improve the maintenance of stem cell distributions to create balanced populations. A control strategy during each cell division leads to a feedback mechanism involving heterogeneous proliferation that can accelerate regeneration with less fluctuation in the stem cell population. When mutation is allowed, apoptosis evolves to maximize the performance during homeostasis after multiple cell divisions. The overall results highlight the importance of cross-talk between genetic and epigenetic regulation and the performance objectives during homeostasis in shaping a desirable heterogeneous distribution of stem cells in epigenetic states.
Keywords: dynamic programming; fitness function; optimization; robustness; systems biology.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
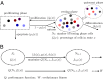
 , or differentiate into other cell types with the probability of
, or differentiate into other cell types with the probability of  . The proliferating cells undergo apoptosis with the probability of
. The proliferating cells undergo apoptosis with the probability of  . Resting phase cells occasionally migrate to the quiescent phase and vice versa under stress. (B) The performance function
. Resting phase cells occasionally migrate to the quiescent phase and vice versa under stress. (B) The performance function  quantifies how well the tissue fits to its physiological properties. The changes in the tissue state
quantifies how well the tissue fits to its physiological properties. The changes in the tissue state  at each cell cycle are determined by the three quantities
at each cell cycle are determined by the three quantities  chosen to maximize the performance at the next cycle to give
chosen to maximize the performance at the next cycle to give  . An evolutionary fitness function at homeostasis, denoted by W, is the limit of
. An evolutionary fitness function at homeostasis, denoted by W, is the limit of  when
when  .
.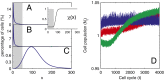
 and
and  are independent of x, and
are independent of x, and  changes with x. (Inset) The performance function
changes with x. (Inset) The performance function  is shown. (B)
is shown. (B)  is independent of x, and
is independent of x, and  and
and  change with x. (C) Both
change with x. (C) Both  and
and  are independent of x, and
are independent of x, and  changes with x. Shadow regions
changes with x. Shadow regions  represent defective states. (D) Time course of Nt under the three conditions (red, green, and blue for conditions A–C, respectively). (See
represent defective states. (D) Time course of Nt under the three conditions (red, green, and blue for conditions A–C, respectively). (See 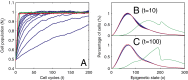
 at
at  cell cycles after the sudden loss. (C) The function
cell cycles after the sudden loss. (C) The function  at
at  cell cycles after the sudden loss. Three different controls are shown: strategy A (red), B (greed), and C (blue). For strategy C, the Hill coefficient m varies from 1 to 10 (from bottom to top in A). The cell populations at homeostasis are normalized to their maximum levels. See
cell cycles after the sudden loss. Three different controls are shown: strategy A (red), B (greed), and C (blue). For strategy C, the Hill coefficient m varies from 1 to 10 (from bottom to top in A). The cell populations at homeostasis are normalized to their maximum levels. See 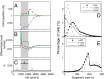
 . (B) Time course of the number of differentiated cells
. (B) Time course of the number of differentiated cells  . (C) Time course of average differentiation
. (C) Time course of average differentiation  . Shadows indicate the time window of increasing differentiation. (D) Cell distributions (strategy A) at three time points (marked with arrows in C), before (filled circles,
. Shadows indicate the time window of increasing differentiation. (D) Cell distributions (strategy A) at three time points (marked with arrows in C), before (filled circles,  ), during (dashed line,
), during (dashed line,  ), and after (solid line,
), and after (solid line,  ) the temporal change of differentiation. (E) Same as D but using strategy B.
) the temporal change of differentiation. (E) Same as D but using strategy B.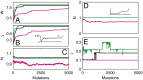
 . Inset shows
. Inset shows  based on strategy B. (C) Cell population N. (D) The cell population when
based on strategy B. (C) Cell population N. (D) The cell population when  is used as the evolutionary fitness. Inset shows the dynamics for strategy B in which the population size markedly increases after 1,000 mutations. (E) Time course of
is used as the evolutionary fitness. Inset shows the dynamics for strategy B in which the population size markedly increases after 1,000 mutations. (E) Time course of  when
when  is used as the evolutionary fitness.
is used as the evolutionary fitness.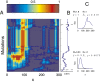
 and the proliferation
and the proliferation  following strategy B. (A) The evolution of
following strategy B. (A) The evolution of  , with the initial
, with the initial  for each x. (B) The proliferation
for each x. (B) The proliferation  that is initiated from
that is initiated from  . (C) The density
. (C) The density  during homeostasis at two time points of mutations, indicated by dashed lines in B. Evolutionary fitness W, population number N, cell performance
during homeostasis at two time points of mutations, indicated by dashed lines in B. Evolutionary fitness W, population number N, cell performance  , and proliferation probability
, and proliferation probability  are also given in each case.
are also given in each case.Comment in
-
Collective dynamics of stem cell populations.Proc Natl Acad Sci U S A. 2014 Mar 11;111(10):3653-4. doi: 10.1073/pnas.1401030111. Epub 2014 Mar 3. Proc Natl Acad Sci U S A. 2014. PMID: 24591612 Free PMC article. No abstract available.
Similar articles
-
Collective dynamics of stem cell populations.Proc Natl Acad Sci U S A. 2014 Mar 11;111(10):3653-4. doi: 10.1073/pnas.1401030111. Epub 2014 Mar 3. Proc Natl Acad Sci U S A. 2014. PMID: 24591612 Free PMC article. No abstract available.
-
A mathematical model of stem cell regeneration with epigenetic state transitions.Math Biosci Eng. 2017 Oct/Dec 1;14(5-6):1379-1397. doi: 10.3934/mbe.2017071. Math Biosci Eng. 2017. PMID: 29161866
-
A general mathematical framework for understanding the behavior of heterogeneous stem cell regeneration.J Theor Biol. 2020 May 7;492:110196. doi: 10.1016/j.jtbi.2020.110196. Epub 2020 Feb 14. J Theor Biol. 2020. PMID: 32067937
-
Molecular regulation of stem cell quiescence.Nat Rev Mol Cell Biol. 2013 Jun;14(6):329-40. doi: 10.1038/nrm3591. Nat Rev Mol Cell Biol. 2013. PMID: 23698583 Free PMC article. Review.
-
Cellular mechanisms of somatic stem cell aging.Curr Top Dev Biol. 2014;107:405-38. doi: 10.1016/B978-0-12-416022-4.00014-7. Curr Top Dev Biol. 2014. PMID: 24439814 Free PMC article. Review.
Cited by
-
Single cell analysis reveals a biophysical aspect of collective cell-state transition in embryonic stem cell differentiation.Sci Rep. 2018 Aug 10;8(1):11965. doi: 10.1038/s41598-018-30461-2. Sci Rep. 2018. PMID: 30097661 Free PMC article.
-
Bone regeneration strategies: Engineered scaffolds, bioactive molecules and stem cells current stage and future perspectives.Biomaterials. 2018 Oct;180:143-162. doi: 10.1016/j.biomaterials.2018.07.017. Epub 2018 Jul 11. Biomaterials. 2018. PMID: 30036727 Free PMC article. Review.
-
Integrative Analysis of Biomarkers Through Machine Learning Identifies Stemness Features in Colorectal Cancer.Front Cell Dev Biol. 2021 Sep 8;9:724860. doi: 10.3389/fcell.2021.724860. eCollection 2021. Front Cell Dev Biol. 2021. PMID: 34568334 Free PMC article.
-
Feedback control in planarian stem cell systems.BMC Syst Biol. 2016 Feb 13;10:17. doi: 10.1186/s12918-016-0261-8. BMC Syst Biol. 2016. PMID: 26873593 Free PMC article.
-
Synthesizing developmental trajectories.PLoS Comput Biol. 2017 Sep 18;13(9):e1005742. doi: 10.1371/journal.pcbi.1005742. eCollection 2017 Sep. PLoS Comput Biol. 2017. PMID: 28922353 Free PMC article.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

