※チャレンジ問題は4年生時点で理解する必要のない問題です。
※オームの法則(電流×抵抗=電圧)を理解しているとスムーズに解ける部分があり、回路5と回路7に関して使用しています。
回路図
考え方
最初に全ての電球の明るさを確認してから問題を解きます(最後にまとめの表があります)。
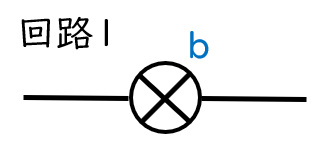
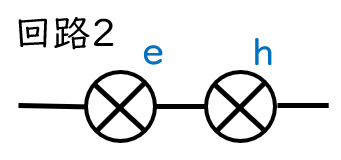
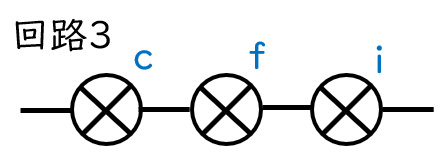
まずは回路1・2・3を見ます。



これらの明るさをここでは回路1=3、回路2=1.5、回路3=1とします。
これらを基準に、他の回路を見ていきます。

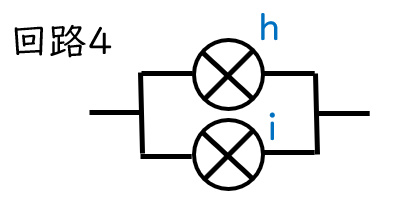
回路4は並列つなぎなので、回路1と同じ明るさになります。よって明るさは3です。

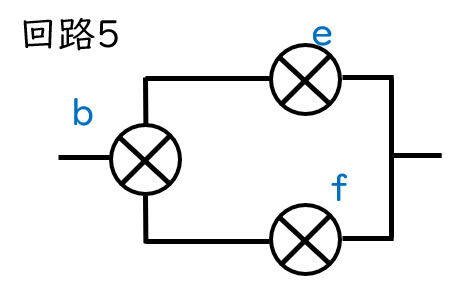
回路5はeとfが並列つなぎなので、まとめて抵抗は0.5となります。
すると回路全体の抵抗はbの1とefの0.5で合わせて1.5となる(豆電球1.5個分を意味する)
ので、回路全体の電流は2となります。(オームの法則より:電流×抵抗=電圧)
並列部分では電流は分散されるので、bの電流が2、efの電流が1となります。
よって明るさは、bが2、efが1です。

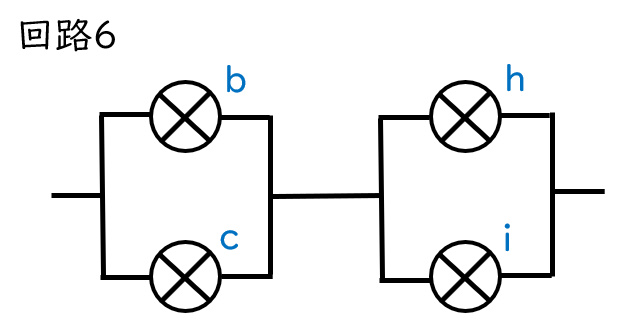
回路6はbとcが並列、hとiが並列なので、並列部分の明るさは豆電球1個の時と変わらないことを考えると、回路2と同じと考えられます。
よって明るさは1.5です。

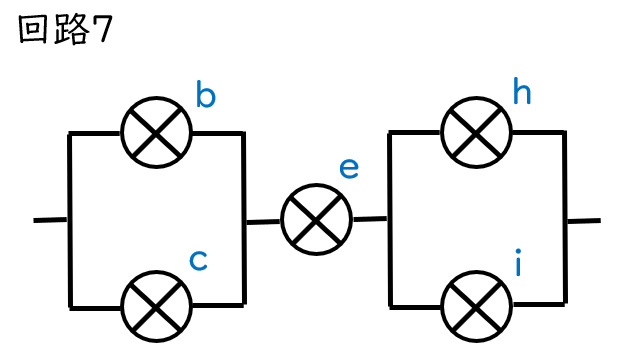
回路7はbc部分の抵抗が0.5、eの抵抗が1,hi部分の抵抗が0.5なので、抵抗の合計は0.5+1+0.5=2です。(豆電球2個分を意味する)
よって回路に流れる電流は1.5。(オームの法則より:電流×抵抗=電圧)
並列部分では電流は分散されるので、bchiの電流が0.75、eの電流が1.5となります。
よってbchiの明るさは0.75、eの明るさは1.5です。
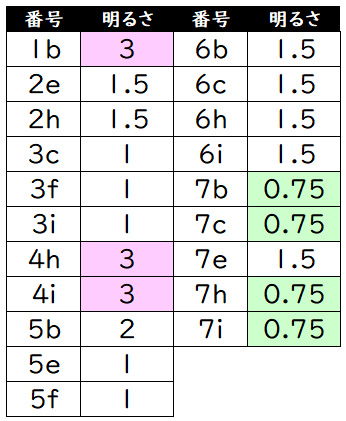
以上をまとめると下表の通りです。
問題の答え
問1:2bは明るさ3なので、同じなのは4hと4i
問2:2eの明るさは1.5なので、同じなのは2h、6b、6c、6h、6i、7eの6個です。
問3:3cの明るさは1なので、同じなのは3f、3i、5e、5fです。
問4:一番明るい明るさは3なので、答えは1b、4h、4iです。
問5:一番暗い明るさは0.75なので、答えは7b、7c、7h、7iです。

コメント