教師あり学習
これは 人工知能アドベントカレンダー の13日目の記事です。
教師あり学習(supervised learning)は、「機械学習といえば教師あり学習」といってもいいくらいの機械学習を代表する一分野で、なにかを認識したり、予想したりするために必要な手法です。ここでは、いくつかの代表的な教師あり学習アルゴリズムを見ていきましょう。
教師あり学習とはなにか
既に度々説明していますが、教師あり学習はデータと正解のペアを与えて、それをもとに学習する方法です。
文字認識(数字認識)を例に取ってみましょう。以下の頭を見てください。
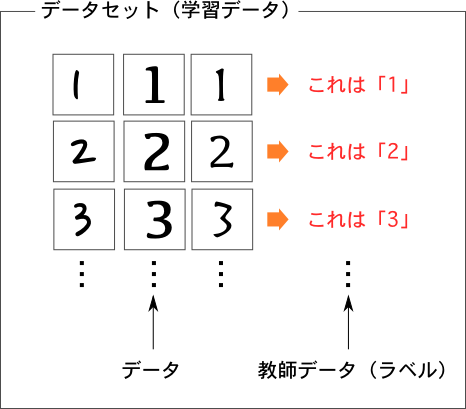
まず、プログラムに教えるためのデータが必要です。いろいろな形の数字の画像をたくさん用意します(図では3つずつしか用意していないが、普通は数百〜数万ほど集める)。そして、それぞれの画像に対して、その画像はどの数字に対応しているのかという正解データも用意します(教師データ、ラベル、教師信号等色々な呼び方がある)。
そしてこのデータとラベルのペアを教師あり学習のプログラム(教師あり学習器、あるいは単に学習器)に与えます。学習器の仕事は、このペアをよく観察して共通する特徴を見つけ出す、つまり「こういう特徴のある画像なら、この数字だ」というルールを見つけることです。
文字認識なら画像を与え、音声認識なら音声を、動画認識なら動画と、その正解を与えればどのようなものでも学習できます*1。
汎化能力
汎化能力(generalization ability)はちょっとここで説明するには難しいのですが、以後も重要な概念になるので簡単に触れておきます。教師あり学習では与えられたデータを学習できても実際には使いものにならないことがあります。たとえば、人間がテスト勉強(ここでは数学を例にする)をするとき、教科書にある問題しか解くことができなくても、その場ではきちんとわかったつもりになれます。ところがテスト本番で、教科書にある問題より少し数字が変わった程度の問題に上手く対応できずにあまり点数がとれなかった、なんて話はよくありますよね。ここでの勉強は、「将来やってくるであろう問題」を解くためにやらなければならないので、逆に言えば教科書にある問題がまったくできなくても、テスト本番で問題が解ければ問題ないといえます。実際には、例題も解けないのに試験で上手く出来るとは思えないので両者は別物ではないのですが、教師あり学習でも同じことがいえます。
教師あり学習では、人間が用意した学習データはちゃんと認識できてるのに、いざ実際に使おうと思うと未知のデータにまったく対応できていない、ということが非常によくあります(過学習, overfitting)。これをクリアして、予め用意しておいたデータもちゃんと正解できるし、新たな未知のデータもきちんと正解できる学習器のことを「汎化能力が高い」といいます。教師あり学習の歴史は結局のところ、いかに過学習せずに汎化能力を高めるかという歴史にほかなりません。
代表的な手法
教師あり学習のアルゴリズムは非常に幅広く、また一見別物だが数学的には非常に似てる、とか、複数のアルゴリズムを組み合わせたアルゴリズム、などもあるので、すっきりとした分類は難しいのですが、そのような細かい点はある程度注釈に書くことにして、よく挙げられる(あるいは使われている)アルゴリズムをいくつか紹介します。
ニューラルネットワーク
いきなり本命のニューラルネットワークです。ただニューラルネットワークは1950年代には既に登場していて*2、この頃はまだC言語もLISPもないどころかようやくトランジスタが実用化されつつあるといった時代です。今ディープラーニングに牽引されて大ブームのニューラルネットワークですが、割と初期の頃から注目はされていたわけです。
しかも、他の手法も広義のニューラルネットワークとして扱えるものが多く、なんでもありな手法ではあります。
SVM
SVM(サポートベクターマシン, Support Vector Machine)は1963年に基本的なアイディアが、1992年に改良したものが発表され、特に改良後のカーネル法を使ったSVMという手法は当時とてつもない性能を誇り、今で言うDeepLearningブームのようになんでもSVMで学習すればOKという、教師あり学習のデファクトスタンダードな存在になりました。今でもSVMは非常によく使われていて、Deep Learningと組み合わせる手法も一般的です。SVMはその頃様々な問題が指摘されて下火になりかけていたニューラルネットワークにトドメを刺してDeep Learning誕生まで王者のように君臨していたレベルのアルゴリズムなので、ここでももう少しだけ詳しく触れておきましょう。

上のような問題を考えます。白と黒のデータがあって、それを分割する線を引きたいのです。いったん線が引ければ、新しいデータがきたときに、線のどちらがわにあるかどうか見るだけで、未知のデータが白なのか黒なのか当てることができます。これが目的です。実用的には白丸と黒丸ではなくて、それが数字データだったりするわけですが、ここでは簡単のために2次元平面上に黒丸か白丸があるというシンプルな問題を考えます。
でも、線の引き方には無数のパターンが考えられます(図右)。ここで、どう線を引くかで汎化能力が変わるので、過学習しないように、汎化能力が最も高くなるようなところに線を引きたいところです。
SVMでは、次のような考え方で線を引きます。白のデータと黒のデータの集まりから、お互い最も近いデータを見つけます(図では二重丸で示したデータ)。そしてそのデータから最も離れた場所に線を引くのです(青線)。

これをSVMではマージン最大化(maximum margin)と呼ぶのですが、このような基準でわけると大抵うまくいくことがわかっています。まあ直感的にも、複数のデータを分割するときは、その真ん中あたりで分割するのが合理的に思えますよね。
ただ、SVMはまっすぐな線しか引けないので、次のようなデータのときは困ってしまいます。

こういう学習データはどう頑張っても直線できれいに区切ることができません*3。ここまでが最初に提案されたSVMで、「まっすぐな線で区切れるような性質のデータならいいけど、そうじゃないと…」という微妙なしこりが残る手法でした。ところが1992年に革命的なアイディアでこれを乗り切ることに成功しました。ここでは難しい話を飛ばして、視覚的にわかりやすい説明をします。

上の図を見てください。「まっすぐな線でしか区切れないなら、データがある空間のほうを捻じ曲げよう」というメチャクチャな方法です。直線で区切れないデータでも、空間をうまく曲げると区切れるデータに変えることができます(図の赤線)。「そんなにうまい方法があるものか」と思ってしまいますが、カーネル関数を使うことで都合のいい空間を考えることが出来る上に、カーネルトリック(kernel trick)という方法も編み出され、カーネルトリックを使うと難しい計算を飛ばして、簡単に処理することができます*4。
この謎の空間でSVMを使ってまっすぐな線をひいた後に、もとの空間に戻ってくると、あら不思議、直線を引いたはずなのに曲線になっています…というようなアルゴリズムです。よくわかりませんよね。実際にSVMの理論はとてもむずかしいのですが、とにかくすごい方法なのです*5。

決定木
決定木(decision tree)はSVMと比べるとずいぶんわかりやすい手法です。ここでは実利を兼ね備えた例題として、「(食べ物の)ニラとスイセンを見分ける学習器を作る」ことを目標にしていることにしましょう*6。

類を見ないほどに利便性の高い決定木の例
見て分かる通り、決定木はデータが与えられた時に、ある条件を満たしているかどうか?でどんどん分岐していって最終的な出力を行う方法です。
当然、これらの属性は予め人が決めておくわけですが、決定木は図のような木構造を自動的に決めてくれます。
最初に「ニラの匂いがするか」という質問が来ていますが、決定木は一番確実そうな*7ものから質問していきます。最後の方になると茎の太さというあんまり確実性がなさそうな質問になっていきます。
決定木のとても良いところは、他の手法と異なり、結果が人間が理解できる形で出力されることです。先ほどの図を見てもお分かりの通り、人間にとってとてもわかりやすい形式で学習器を出力してくれます。また、単に「はい/いいえ」で答えられるようなものと、「1cm以上かどうか」といったある閾値を設けて振り分けていく方法をどちらも混ぜて使えるのも、他の手法ではあまりない決定木のメリットです。
ここから派生したアルゴリズムとして、Random Forest や xgboost があり、これらは色々な決定木を大量につくって、多数決で最終的な答えを決めるものです。こちらはその性質上時間がかかるのはデメリットなのですが、扱いやすく精度も高いので色々なところで使われています(たとえばMicrosoftのKinectが有名な例)。
Random Forest 系のアルゴリズムは、以前のブログで扱ったことがあるので、興味のある方は御覧ください。
線形分類器たち
線形分類器は、データを直線で区切るアルゴリズムすべてを指すので、実はSVMも線形分類器です*8。ただSVMは歴史的にも実用的にも機械学習に大きな影響を及ぼしたので、別途枠を設けました。
すでにSVMの項目で、「データを直線で区切れないデメリットがある」と言ってしまった線形分類器ですが、意外にも実用的にはかなり使えるアルゴリズムです。詳しい理由は省きますが、
- 学習も認識も高速
- オンライン学習しやすい*9
- 意外と線形分離できるデータが多い*10
- Kernelと組み合わせることで線形分類器でも非線形分離ができる(曲線で区切れる)ので実用上問題ない
- アルゴリズムがシンプルで使いやすい
- よく研究されていて、理論的なバックグラウンドが盤石
実は線形分類器についても過去のブログで取り扱っているので、興味のある方はそちらも御覧ください。
線形分類器はとくかく色々な種類があるのですべて紹介しきれませんが、古くはパーセプトロンやSVM、最近でも活発に研究されていて、AROWやSCWといった方法が提案されています。実用例としては、GMailの優先トレイ(重要と思われるメールが目立つように表示される機能)は線形分類器のひとつである Passive Aggressive で実装されていたようです(今は改善されて違う方法かもしれません)。
分類と回帰
具体例として上げたのは「0〜9までのどの文字か?」「黒丸か白丸か」「ニラとスイセンのどちらか?」といったどれかに分類するものでしたが、実際には回帰といって、数値を出すこともできます。たとえば、顔写真から年齢を推定したいときは、「0歳か1歳か2歳か3歳か4歳か…」といった分類方法でもダメではないのですが、回帰を使うと「25.3歳」のように実数を出力してくれます。天気も「晴れか曇りか雨かを予想したい」場合は分類になりますが、「明日の気温が何度になるか予想したい」場合は回帰になります。
あるいは株価のデータを使って、「株価が上がる確率はいくらか」といった確率を扱う場合も回帰が利用できます。回帰をそのまま分類に使うこともできるので両者の違いはたまに曖昧なのですが*11、分類も回帰も応用範囲が広いのでよく利用されます。
まとめ
教師あり学習は非常に重要な役割を果たし、また画像認識、音声認識など最近良く話題になる分野なので、すこし雑多になってしまいましたが、いつもより細かく紹介してみました。人間の脳も、ある種の教師あり学習をしているという見方が有力ですが、これはまた後日詳しく見ていくことにしましょう。
*1:これはかなり不正確な表現で、どのようなデータでも人間が適切に設計された特徴ベクトルに変換できれば学習できる、ということ
*4:これ以上詳しく説明しようとすると、また1ヶ月分のアドベントカレンダーが必要になるので、カーネルや再生核ヒルベルト空間の話はここではしないし、高次元空間への写像なども触れない
*5:最近はSVMやKernel法に関するやさしい解説がインターネットにも多くあるので、気になった人は見てみることをおすすめします。細かい証明を考えなければ、カーネルやカーネルトリックの考え方はそれなりにわかりやすいかと思います
*6:ニラとスイセンは見た目が似ているため、間違って庭に生えている有毒なスイセンを食べてしまう事故がよくある
*7:具体的な決め方はアルゴリズムによるが、GINI係数を使うCARTなどが有名
*8:もっと言えば、線形分類器はニューラルネットワークで表現できるので、線形分類器もSVMもニューラルネットワークのひとつだとも言える。ただ、あまり一般的な分類ではない。
*9:オンライン学習は、データをいっぺんに与える必要がなく、必要なときに適時追加していくような使い方ができるアルゴリズム
*10:これも詳しい理由は省くが、自然言語処理などは非常に高次元なデータを扱う事が多く、そのようなデータは線形分離可能なことが多い
*11:ロジスティック回帰などがその例